题目内容
10.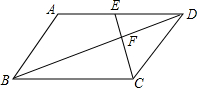 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$.
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$.
分析 先根据平行四边形的性质得到AD∥BC,AD=BC,再由点E是边AD的中点得到DE=$\frac{1}{2}$BC,接着证明△DEF∽△BCF,然后根据相似三角形的性质求解.
解答 解:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
∵点E是边AD的中点,
∴DE=$\frac{1}{2}$BC,
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{{S}_{△DEF}}{S△BCF}$=($\frac{DE}{BC}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.在利用相似三角形的性质时,注意通过相似比计算相应线段的长或对应角线段.解决本题的关键是利用平行四边形的性质对边平行而构建相似三角形.

练习册系列答案
相关题目
8.如果关于x的方程(m-1)x2+x+1=0有实数根,那么m的取值范围是( )
| A. | $m<\frac{5}{4}$ | B. | $m<\frac{5}{4}$且m≠1 | C. | $m≤\frac{5}{4}$ | D. | $m≤\frac{5}{4}$且m≠1 |
1.抛物线y=-x2+3x-2与坐标轴的交点共有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20. 如图,要使平行四边形ABCD成为菱形,需添加的一个条件是( )
如图,要使平行四边形ABCD成为菱形,需添加的一个条件是( )
 如图,要使平行四边形ABCD成为菱形,需添加的一个条件是( )
如图,要使平行四边形ABCD成为菱形,需添加的一个条件是( )| A. | AB=BC | B. | AC=BD | C. | ∠ABC=90° | D. | AC与BD互相平分 |
 如图,在△ABC中,已知D是边AB上的一点,连接CD,那么还需要增加一个条件∠ACD=∠B(答案不唯一),才能使△ACD∽△ABC.
如图,在△ABC中,已知D是边AB上的一点,连接CD,那么还需要增加一个条件∠ACD=∠B(答案不唯一),才能使△ACD∽△ABC. 如图,△OAD≌△OBC,且∠O=60°,∠C=20°,则∠OAD=100°.
如图,△OAD≌△OBC,且∠O=60°,∠C=20°,则∠OAD=100°. 如图,△ABC与△A′B′C′关于直线对称,则∠B的度数为105°.
如图,△ABC与△A′B′C′关于直线对称,则∠B的度数为105°.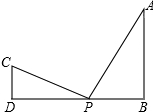 如图,AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,点P在DB上移动.若以点C,D,P为顶点的三角形与点A,B,P为顶点的三角形相似,则DP=2或12或5.6.
如图,AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,点P在DB上移动.若以点C,D,P为顶点的三角形与点A,B,P为顶点的三角形相似,则DP=2或12或5.6. 如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,则抛物线y2的顶点坐标为(1,2);阴影部分的面积S=2.
如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,则抛物线y2的顶点坐标为(1,2);阴影部分的面积S=2.