题目内容
1．抛物线y=-x2+3x-2与坐标轴的交点共有（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 计算自变量为0时的函数值可得到抛物线与y轴的交点坐标，通过解方程-x2+3x-2=0可得到抛物线与x轴的交点坐标，于是可判断抛物线y=-x2+3x-2与坐标轴的交点个数．
解答 解：当x=0时，y=-x2+3x-2=-2，则抛物线与y轴相交于点（0，-2），
当y=0时，-x2+3x-2=0，解得x1=1，x2=2，则抛物线与x轴的交点坐标为（1，0），（2，0）．
故选D．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．
练习册系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
已知点A（0，3），B（-1，1），C（-3，2），D（-2，0），E（-3，-2），F（-1，-1），G（0，-3），H（1，-1），I（3，-2），J（2，0），K（3，2），L（1，1）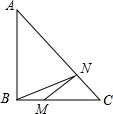
如图，在Rt△ABC中，∠ABC=90°，AB=BC=4，点M在BC上，且BM=1，N是AC上一动点，则BN+MN的最小值为5．
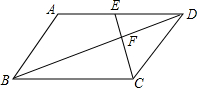如图，在?ABCD中，点E是边AD的中点，EC交对角线BD于点F，则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$．