题目内容
2.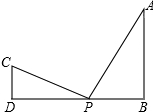 如图,AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,点P在DB上移动.若以点C,D,P为顶点的三角形与点A,B,P为顶点的三角形相似,则DP=2或12或5.6.
如图,AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,点P在DB上移动.若以点C,D,P为顶点的三角形与点A,B,P为顶点的三角形相似,则DP=2或12或5.6.
分析 分别从若△PCD∽△APB与若△PCD∽△PAB去分析求解,根据相似三角形的对应边成比例,即可求得答案.
解答 解:∵①若△PCD∽△APB,则$\frac{CD}{PB}=\frac{DP}{AB}$,即$\frac{4}{14-DP}=\frac{DP}{6}$,解得DP=2或12;
②若△PCD∽△PAB,则$\frac{CD}{AB}=\frac{DP}{PB}$,即$\frac{4}{6}=\frac{DP}{14-DP}$,解得DP=5.6.
∴DP=2或12或5.6.
故答案为:2或12或5.6.
点评 此题考查了相似三角形的性质.注意分类讨论思想的应用是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列现象属于旋转的是( )
| A. | 摩托车在急刹车时向前滑动 | B. | 飞机起飞后冲向空中的时候 | ||
| C. | 笔直的铁轨上飞驰而过的火车 | D. | 幸运大转盘转动的过程 |
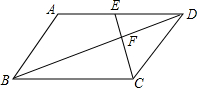 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$.
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$. 如图,在△ABC中,∠C=90°,BD是∠ABC的平分线且BD=4.若BC=3,则点D到AB的距离是$\sqrt{7}$.
如图,在△ABC中,∠C=90°,BD是∠ABC的平分线且BD=4.若BC=3,则点D到AB的距离是$\sqrt{7}$.