题目内容
8.如果关于x的方程(m-1)x2+x+1=0有实数根,那么m的取值范围是( )| A. | $m<\frac{5}{4}$ | B. | $m<\frac{5}{4}$且m≠1 | C. | $m≤\frac{5}{4}$ | D. | $m≤\frac{5}{4}$且m≠1 |
分析 分类讨论:当m-1=0时,方程为一元一次方程,有解;当m-1≠0时,根据判别式的意义得到△=12-4×(m-1)×1≥0,解得m≤$\frac{5}{4}$且m≠1,然后综合两种情况就看得到m的取值范围.
解答 解:当m-1=0时,x+1=0,解得x=-1;
当m-1≠0时,△=12-4×(m-1)×1≥0,解得m≤$\frac{5}{4}$且m≠1,
所以m的取值范围为m≤$\frac{5}{4}$.
故选C.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
 已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K(3,2),L(1,1)
已知点A(0,3),B(-1,1),C(-3,2),D(-2,0),E(-3,-2),F(-1,-1),G(0,-3),H(1,-1),I(3,-2),J(2,0),K(3,2),L(1,1)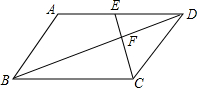 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$.
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=$\frac{1}{4}$.