题目内容
 如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.
如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:利用平行线的性质结合翻折变换的性质得出∠EFC=∠EFH=120°,即可得出答案.
解答:
解:∵四边形ABCD是长方形,∠EFD=80°,
∴AB∥DC,∠BEF=80°,
∴∠EFC=∠EFH=120°,
∴∠DFH的度数为:120°-80°=40°.
∴AB∥DC,∠BEF=80°,
∴∠EFC=∠EFH=120°,
∴∠DFH的度数为:120°-80°=40°.
点评:此题主要考查了平行线的性质以及翻折变换的性质等知识,得出∠EFC=∠EFH=120°是解题关键.

练习册系列答案
相关题目
若点A(2a-1,5-a)到两坐标轴的距离相等,则点A的坐标是( )
| A、(3,3) |
| B、(-9,9) |
| C、(3,3)或(-9,9) |
| D、不确定 |
在反比例函数y=
(k<0)的图象上有两点,(-1,y1),(-
,y2),则y1-y2的值是( )
| k |
| x |
| 1 |
| 4 |
| A、正数 | B、非正数 |
| C、负数 | D、不能确定 |
若
+
有意义,则x应满足的条件是( )
| x-1 |
| 1-x |
| A、x≥1 | B、x≤1 |
| C、x=1 | D、x≠1 |
 如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求:
如下图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBC,∠DBA是什么角时,满足下列要求: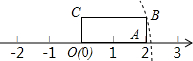 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( ) 一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.