题目内容
若点A(2a-1,5-a)到两坐标轴的距离相等,则点A的坐标是( )
| A、(3,3) |
| B、(-9,9) |
| C、(3,3)或(-9,9) |
| D、不确定 |
考点:点的坐标
专题:
分析:根据点到两坐标轴的距离相等列出绝对值方程,然后求出a的值,再求解即可.
解答:
解:∵点A(2a-1,5-a)到两坐标轴的距离相等,
∴|2a-1|=|5-a|,
∴2a-1=5-a或2a-1=-(5-a),
解得a=2或a=-4,
当a=2时,2a-1=2×2-1=3,
此时,点A的坐标为(3,3),
当a=-4时,2a-1=2×(-4)-1=-9,
此时,点A的坐标为(-9,9),
综上所述,点A的坐标为(3,3)或(-9,9).
故选C.
∴|2a-1|=|5-a|,
∴2a-1=5-a或2a-1=-(5-a),
解得a=2或a=-4,
当a=2时,2a-1=2×2-1=3,
此时,点A的坐标为(3,3),
当a=-4时,2a-1=2×(-4)-1=-9,
此时,点A的坐标为(-9,9),
综上所述,点A的坐标为(3,3)或(-9,9).
故选C.
点评:本题考查了点的坐标,是基础题,难点在于列出绝对值方程并求出a的值.

练习册系列答案
相关题目
下列图形中,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
将抛物线y=x2先向右平移2个单位,再向下平移3个单位,那么得到的新的抛物线的解析式是( )
| A、y=(x+2)2+3 |
| B、y=(x+2)2-3 |
| C、y=(x-2)2+3 |
| D、y=(x-2)2-3 |
对于函数y=x2,下列结论正确的是( )
| A、图象的开口向下 |
| B、y随x增大而增大 |
| C、图象关于y轴对称 |
| D、对于任意实数,都有y>0 |
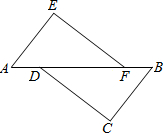 如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:
如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证: 如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.
如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?