题目内容
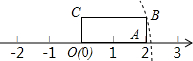 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )A、
| ||
B、2
| ||
C、
| ||
| D、2.5 |
考点:实数与数轴
专题:
分析:利用勾股定理列式求出OB,然后根据数轴写出点所表示的数即可.
解答:
解:∵矩形OABC的长OA为2,宽AB为1,
∴由勾股定理得,OB=
=
=
,
∴这个点表示的示数是
.
故选C.
∴由勾股定理得,OB=
| OA2+AB2 |
| 22+12 |
| 5 |
∴这个点表示的示数是
| 5 |
故选C.
点评:本题考查了勾股定理,实数与数轴,主要是无理数在数轴上的表示,熟记定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形网格中,有a、b、c、d四条线段,其中能由a平移得到的线段是( )
如图,正方形网格中,有a、b、c、d四条线段,其中能由a平移得到的线段是( )| A、b | B、c |
| C、d | D、b、c、d都可以 |
对于函数y=x2,下列结论正确的是( )
| A、图象的开口向下 |
| B、y随x增大而增大 |
| C、图象关于y轴对称 |
| D、对于任意实数,都有y>0 |
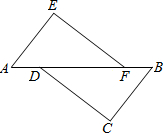 如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证:
如图,A、D、F、B在同一直线上,AF=BD,AE=BC,且AE∥BC.求证: 如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.
如图所示,将长方形ABCD沿EF折叠,使点B落在点G,点C落在点H处,若∠EFD=80°,求∠DFH的度数.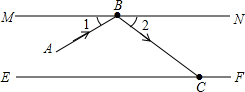 如图,MN,EF是两个互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
如图,MN,EF是两个互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律: 如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.