题目内容
18.已知Rt△ABC中,∠C=90°,D、E分别AC、AB的中点,连接DE,并延长到点F,使EF=EB,过点F作FG⊥AB于点G,连接DG并延长,交CB的延长线于点H,连接FH,给出以下四个结论:①∠FGH=∠CDG;②DE=GE;③$\frac{EG}{DC}=\frac{FG}{CH}$;④四边形CDFH是矩形其中正确的结论有①②④.(把你认为正确结论的序号都填上)
分析 根据△ADE≌△FGE,即可得到DE=GE,根据等角的余角相等即可得出∠CDG=∠FGH,根据△HCD与△FGE不一定相似,可得$\frac{EG}{DC}=\frac{FG}{CH}$不一定成立,根据∠FGB=∠FHB=90°,∠C=∠CDF=90°,即可得到四边形CDFH是矩形.
解答  解:∵D、E分别AC、AB的中点,
解:∵D、E分别AC、AB的中点,
∴DE∥BC,
∵∠C=90°,
∴∠ADE=90°,
又∵FG⊥AB,
∴∠FGE=∠ADE=90°,
∵EF=EB,EB=AE,
∴AE=FE,
在△ADE和△FGE中,
$\left\{\begin{array}{l}{∠FGE=∠ADE}\\{∠AED=∠FEG}\\{AE=FE}\end{array}\right.$,
∴△ADE≌△FGE(AAS),
∴DE=GE,故②正确;
∴∠EDG=∠EGD,
又∵∠CDG+∠EDG=90°,∠FGH+∠EGD=90°,
∴∠CDG=∠FGH,故①正确;
∵△ADE≌△FGE,
∴∠A=∠EFG,
又∵∠CHD与∠A不一定相等,
∴∠CHD与∠EFG不一定相等,
而∠EFG与∠CDH也不一定相等,
∴△HCD与△FGE不一定相似,
∴$\frac{EG}{DC}=\frac{FG}{CH}$不一定成立,故③错误;
如图,连接BF,
∵BH∥DE,
∴∠GHB=∠EDG=∠EGD=∠BGH,∠FBH=∠BFE,
∴BG=BH,
∵EB=EF,
∴∠BFE=∠FBG,
∴∠FBG=∠FBH,
在△FBG和△FBH中,
$\left\{\begin{array}{l}{BG=BH}\\{∠FBG=∠FBH}\\{BF=BF}\end{array}\right.$,
∴△FBG≌△FBH(SAS),
∴∠FGB=∠FHB=90°,
又∵∠C=∠CDF=90°,
∴四边形CDFH是矩形,故④正确,
故答案为:①②④.
点评 本题主要考查了矩形的判定,全等三角形的判定与性质,三角形中位线定理以及相似三角形的判定与性质的综合应用,解决问题的关键是判定三角形全等,依据全等三角形的对应边相等,对应角相等作出判断.

 阅读快车系列答案
阅读快车系列答案 如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )| A. | 16 cm | B. | 18 cm | C. | 20 cm | D. | 21 cm |
| A. |  | B. |  | C. |  | D. |  |
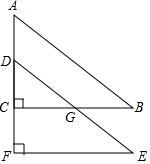 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6cm,将△ABC沿着AC方向平移2cm得△DEF,DE交BC于点G,则四边形CGEF的面积为10$\sqrt{3}$cm2.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6cm,将△ABC沿着AC方向平移2cm得△DEF,DE交BC于点G,则四边形CGEF的面积为10$\sqrt{3}$cm2.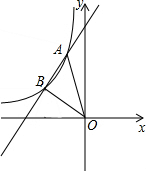 一次函数y=x+5的图象与反比例函数y=$\frac{k}{x}$(k<0)在第二象限的图象交于A(-1,n)和B两点.
一次函数y=x+5的图象与反比例函数y=$\frac{k}{x}$(k<0)在第二象限的图象交于A(-1,n)和B两点.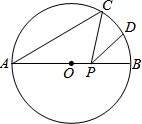 如图,AB是⊙O的直径,AB=10,∠A=40°,点D为弧BC的中点,点P是直径AB上的一个动点,PC+PD的最小值为5$\sqrt{3}$.
如图,AB是⊙O的直径,AB=10,∠A=40°,点D为弧BC的中点,点P是直径AB上的一个动点,PC+PD的最小值为5$\sqrt{3}$.