Question

7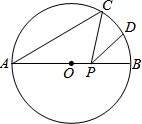．如图，AB是⊙O的直径，AB=10，∠A=40°，点D为弧BC的中点，点P是直径AB上的一个动点，PC+PD的最小值为5$\sqrt{3}$．

Answer 1

分析 作出D关于AB的对称点D′，则PC+PD的最小值就是CD′的长度，在△COD′中根据边角关系即可求解．

解答 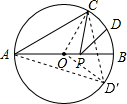解：作出D关于AB的对称点D′，连接OC，OD′，CD′．
又∵点C在⊙O上，∠CAB=40°，D为$\widehat{BC}$的中点，即$\widehat{BD}$=$\widehat{BD′}$，
∴∠BAD′=$\frac{1}{2}$∠CAB=20°．
∴∠CAD′=60°．
∴∠COD′=120°，
∵OC=OD′=$\frac{1}{2}$AB=5，
∴CD′=5$\sqrt{3}$．
故答案为：5$\sqrt{3}$．

点评 本题考查了圆周角定理以及路程和最小的问题，正确作出辅助线是解题的关键．