题目内容
6.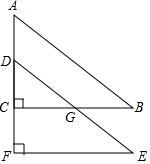 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6cm,将△ABC沿着AC方向平移2cm得△DEF,DE交BC于点G,则四边形CGEF的面积为10$\sqrt{3}$cm2.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6cm,将△ABC沿着AC方向平移2cm得△DEF,DE交BC于点G,则四边形CGEF的面积为10$\sqrt{3}$cm2.
分析 根据直角三角形两锐角互余求出∠B=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AB,再利用勾股定理列式求出BC,然后求出△ABC的面积,从而得到△DEF的面积,再求出CD,同理求出DG、CG,然后求出△CDG的面积,最后根据S四边形CGEF=S△DEF-S△CDG列式计算即可得解.
解答 解:∵∠ACB=90°,∠A=60°,
∴∠B=90°-60°=30°,
∴AB=2AC=2×6=12cm,
在Rt△ABC中,根据勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$cm,
∴S△ABC=$\frac{1}{2}$×6$\sqrt{3}$×6=18$\sqrt{3}$cm2,
∵△ABC沿着AC方向平移2cm得△DEF,
∴S△DEF=S△ABC=18$\sqrt{3}$cm2,
由平移得,AD=2cm,
所以,CD=6-2=4cm,
同理可得,DG=2CD=8cm,
CG=4$\sqrt{3}$cm,
所以,S△CDG=$\frac{1}{2}$×4$\sqrt{3}$×4=8$\sqrt{3}$cm2,
所以,S四边形CGEF=S△DEF-S△CDG=18$\sqrt{3}$-8$\sqrt{3}$=10$\sqrt{3}$cm2.
故答案为:10$\sqrt{3}$.
点评 本题考查了平移的性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.还考查了直角三角形30°角所对的直角边等于斜边的一半的性质.

练习册系列答案
相关题目
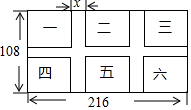 如图,宏达蔬菜基地内有一块长为216m,宽为108m的长方形土地,三条宽均为xm的田间小路把它分成面积相等的六块,分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子.
如图,宏达蔬菜基地内有一块长为216m,宽为108m的长方形土地,三条宽均为xm的田间小路把它分成面积相等的六块,分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子.