题目内容
一次函数y=-ax+b的图象经过第二、三、四象限,化简:
-
.
| (a-b)2 |
| b2 |
考点:一次函数图象与系数的关系
专题:
分析:由于一次函数y=ax+b的图象经过第二、三、四象限,由此可以确定a<0,b<0,然后根据|a|与|b|的大小来确定(a-b)的符号.
解答:解:∵一次函数y=-ax+b的图象经过第二、三、四象限,
∴a<0,b<0.
①当|a|≥|b|时,a-b≤0,
-
=|a-b|-|b|=b-a+b=2b-a;
②当|a|<|b|时,a-b>0,
-
=|a-b|-|b|=a-b+b=a;
综上所述,
-
=2b-a或
-
=a.
∴a<0,b<0.
①当|a|≥|b|时,a-b≤0,
| (a-b)2 |
| b2 |
②当|a|<|b|时,a-b>0,
| (a-b)2 |
| b2 |
综上所述,
| (a-b)2 |
| b2 |
| (a-b)2 |
| b2 |
点评:此题主要考查了一次函数的图象的性质,首先根据图象经过的象限确定a、b的符号,然后即可解决题目的问题.

练习册系列答案
相关题目
如果点A(1,2)在直线y=3x+b上,则b的值为( )
| A、-1 | B、2 | C、3 | D、5 |
下列说法正确的是( )
A、在Rt△ABC中,sinA=
| ||
B、在△ABC中,sinA=
| ||
| C、在Rt△ABC中,0<sinA≤1 | ||
| D、在Rt△ABC中,sinA=sinB |
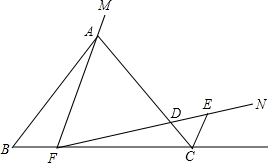 如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想.
如图,△ABC是等边三角形,点F在直线BC上,∠MFN=60°,∠MFN的一边FM始终过△ABC的顶点A,另一边FN与△ABC的外角平分线交于点E,当点F在BC的任意位置时,写出关于线段FA、FE的数量关系的猜想,并证明你的猜想. 已知AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是
已知AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是