题目内容
4.求下列不等式组的解集并在下面的数轴上表示出来(1)$\left\{\begin{array}{l}{2x>x+1}\\{3x+7≥x-1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x-2>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$
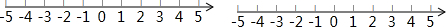
分析 (1)、(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)$\left\{\begin{array}{l}2x>x+1①\\ 3x+7≥x-1②\end{array}\right.$,由①得,x>1,由②得,x≥-4,故不等式组的解集为:x>1,
在数轴上表示为: ;
;
(2)$\left\{\begin{array}{l}5x-2>3(x+1)①\\ \frac{1}{2}x-1≤7-\frac{3}{2}x②\end{array}\right.$,由①得,x>$\frac{5}{2}$,由②得,x≤4,故不等式组的解集为:$\frac{5}{2}$<x≤4,
在数轴上表示为: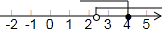 .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
9.下列等式正确的有( )
①a4b2=(ab)6; ②(10n+1)2=102n+2;③25+25=210; ④${({x^n})^n}•{x^n}={x^{{n^2}+n}}$.
①a4b2=(ab)6; ②(10n+1)2=102n+2;③25+25=210; ④${({x^n})^n}•{x^n}={x^{{n^2}+n}}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列各式正确的是( )
| A. | $\sqrt{{{(-5)}^2}}=-5$ | B. | $-\sqrt{{{(-15)}^2}}=-15$ | C. | $\sqrt{{{(-5)}^2}}=±5$ | D. | $\sqrt{\frac{1}{2}}=\frac{1}{2}$ |
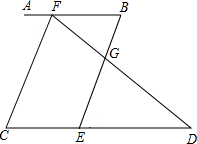 已知:如图,∠C=∠BED,∠AFC和∠D互余,BE⊥FD与G.
已知:如图,∠C=∠BED,∠AFC和∠D互余,BE⊥FD与G.