题目内容
12.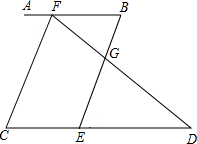 已知:如图,∠C=∠BED,∠AFC和∠D互余,BE⊥FD与G.
已知:如图,∠C=∠BED,∠AFC和∠D互余,BE⊥FD与G.证明:AB∥CD.
分析 由互余的定义,可得:∠AFC+∠D=90°,由垂直的定义可得:∠EGD=90°,然后根据三角形内角和定理可得:∠BED+∠D=90°,然后根据等量代换可得:∠AFC=∠BED,由∠C=∠BED,根据等量代换可得:∠C=∠AFC,然后根据内错角相等两直线平行可得:AB∥CD
解答 证明:∵∠AFC和∠D互余.(已知)
∴∠AFC+∠D=90°(余角之和为90°)
∵BE⊥FD(已知)
∴∠EGD=90°(垂直的定义)
即∠BED+∠D=90°(三角形之和等于180°)
∴∠AFC=∠BED(等量代换)
∵∠C=∠BED(已知)
∴∠C=∠AFC(等量代换)
∴AB∥CD(内错角相等,两直线平行).
点评 此题考查了平行线的判定,解题的关键是:熟记同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行.

练习册系列答案
相关题目
20.方程组$\left\{\begin{array}{l}{3x-4y=2}\\{x+2y=1}\end{array}\right.$用代入法消去x,所得y的一元一次方程为( )
| A. | 3-2y-1-4y=2 | B. | 3(1-2y)-4y=2 | C. | 3(2y-1)-4y=2 | D. | 3-2y-4y=2 |