题目内容
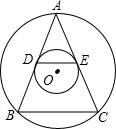 如图所示,已知两个同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC的周长为16cm,求△ADE的周长.
如图所示,已知两个同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC的周长为16cm,求△ADE的周长.考点:切线的性质,相似三角形的判定与性质
专题:计算题
分析:连结OD,OE,如图,先根据切线的性质得AD⊥OD,AC⊥OE,再根据垂径定理得AD=BD,AE=CE,则可判断DE为△ABC的中位线,所以DE=
BC,则△ADE的周长=
(AB+BC+AE)=△ABC的周长的一半.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:连结OD,OE,如图,
∵AB、AC为小圆的切线,
∴AD⊥OD,AC⊥OE,
∴AD=BD,AE=CE,
∴DE为△ABC的中位线,
∴DE=
BC,
∴△ADE的周长=AD+DE+AE
=
(AB+BC+AC)
=
×16
=8cm.

∵AB、AC为小圆的切线,
∴AD⊥OD,AC⊥OE,
∴AD=BD,AE=CE,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
∴△ADE的周长=AD+DE+AE
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=8cm.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理和三角形中位线性质.

练习册系列答案
相关题目
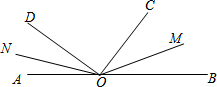 如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=50°,∠BOC=40°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )
如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=50°,∠BOC=40°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )| A、135° | B、140° |
| C、152° | D、45° |
下列成语所描述的事件中是随机事件的是( )
| A、水中捞月 | B、拔苗助长 |
| C、守株待兔 | D、瓮中捉鳖 |
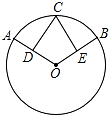 如图,D、E分别是半径OA和OB的中点,
如图,D、E分别是半径OA和OB的中点,
 如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系.
如图,点P是△ABC中两外角∠DBC与∠ECB平分线的交点,试探索∠BPC和∠A的数量关系.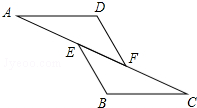 如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.
如图,已知AE=CF,∠AFD=∠CEB,AD∥BC,求证:△ADF≌△CBE.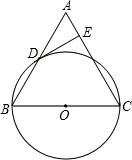 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.