题目内容
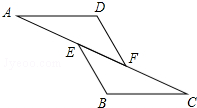如图，已知AE=CF，∠AFD=∠CEB，AD∥BC，求证：△ADF≌△CBE．考点：全等三角形的判定
专题：证明题
分析：证明AF=CE；证明∠A=∠C；运用ASA定理，即可解决问题．
解答：证明：∵AE=CF，
∴AF=CE；
∵AD∥BC，
∴∠A=∠C；
在△ADF与△CBE中，
，
∴△ADF≌△CBE（ASA）．
证明：∵AE=CF，∴AF=CE；
∵AD∥BC，
∴∠A=∠C；
在△ADF与△CBE中，
|
∴△ADF≌△CBE（ASA）．
点评：该题主要考查了全等三角形的判定问题；解题的关键是准确找出图形中的对应元素，灵活选用全等三角形的判定方法．
练习册系列答案
相关题目
在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系，已知格点三角形ABC（三角形的三个顶点都在小正方形上）若n是正整数，则下列各式中正确的是（ ）
| A、（-a）n=-an |
| B、（-a2n+1）=a2n+1 |
| C、（-a）2n=-a2n |
| D、（-a）2n-1=-a2n-1 |
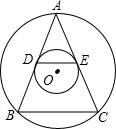如图所示，已知两个同心圆中，大圆的弦AB、AC切小圆于D、E，△ABC的周长为16cm，求△ADE的周长．
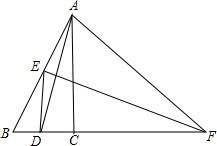如图，已知AD是∠BAC的角平分线，AD的垂直平分线EF交AB于点E，交BC延长线于F．求证：下列运算中正确的是（ ）
| A、2a+3b=5ab | ||
B、3a-2=
| ||
C、（-sin30°）0=-
| ||
| D、（-x5）（-x）3=x8 |