题目内容
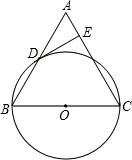 已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论.
考点:切线的判定
专题:证明题
分析:(1)连结CD,如图,根据圆周角定理,由BC为直径得到∠BDC=90°,然后根据等腰三角形的性质得AD=BD;
(2)连结OD,先得到OD为△ABC的中位线,再根据三角形中位线性质得OD∥AC,而DE⊥AC,则DE⊥OD,然后根据切线的判定定理可得DE为⊙O的切线.
(2)连结OD,先得到OD为△ABC的中位线,再根据三角形中位线性质得OD∥AC,而DE⊥AC,则DE⊥OD,然后根据切线的判定定理可得DE为⊙O的切线.
解答: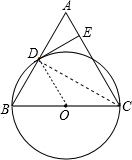 (1)证明:连结CD,如图,
(1)证明:连结CD,如图,
∵BC为直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
即点D是AB的中点;
(2)解:DE与⊙O相切.理由如下:
连结OD,
∵AD=BD,OC=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
而DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线.
 (1)证明:连结CD,如图,
(1)证明:连结CD,如图,∵BC为直径,
∴∠BDC=90°,
∴CD⊥AB,
∵AC=BC,
∴AD=BD,
即点D是AB的中点;
(2)解:DE与⊙O相切.理由如下:
连结OD,
∵AD=BD,OC=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
而DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
将一刻度尺放在数轴上(数轴的单位长度是1cm),使刻度尺上“0cm”和“8cm”分别对应数轴上的-3和x,那么x对应的值可能为( )
| A、5 | B、8 |
| C、-11 | D、5或-11 |
下列运算中正确的是( )
| A、2a+3b=5ab | ||
B、3a-2=
| ||
C、(-sin30°)0=-
| ||
| D、(-x5)(-x)3=x8 |
下列实数中最大的是( )
| A、-2013 | ||
| B、2013 | ||
C、
| ||
D、-
|
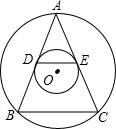 如图所示,已知两个同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC的周长为16cm,求△ADE的周长.
如图所示,已知两个同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC的周长为16cm,求△ADE的周长. 在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73)
在数学课外实践活动中,小于在一条河西岸一段上的A,B两点处利用测角仪分别对东岸的C点进行测量,测得BC与河西岸夹角60°,AC与河西岸夹角75°,且AB=100米,求点C到河西岸的距离.(精确到1米,tan60°≈1.73,tan75°≈3.73) 在物理试验中,当电流在一定时间段内正常通过电子元件
在物理试验中,当电流在一定时间段内正常通过电子元件 时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.当有两个电子元件a、b并联时,P、Q之间电流通过的概率是
时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.当有两个电子元件a、b并联时,P、Q之间电流通过的概率是