题目内容
3.计算:(1)40$\frac{2}{3}$×$39\frac{1}{3}$
(2)(a+b)(a-b)+(a+b)2-2(a-b)2
(3)已知2m=3,4n=2,8k=5,求8m+2n+k的值.
分析 (1)利用平方差公式化简即可.
(2)根据平方差公式或完全平方公式展开,然后合并同类项即可.
(3)逆用幂的乘方公式即可化简.
解答 (1)解:原式=(40+$\frac{2}{3}$0(40-$\frac{2}{3}$)=402-($\frac{2}{3}$)2=1599$\frac{5}{9}$
(2)原式=a2-b2+a2+2ab+b2-2a2+4ab-2b2=6ab-2b2
(3)∵2m=3,4n=2,8k=5,
∴原式=8m×82n×8k=(2m)3×(4n)3×8k=33×23×5=1080.
点评 本题考查整式的混合运算、熟练掌握基本公式是解决问题的关键,学会整体代入的思想,属于展开常考题型.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
15.下列说法正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 互为邻补角的两个角也一定互为补角 | |
| C. | 同垂直于一条直线的两条直线互相平行 | |
| D. | 直线外一点到这条直线的垂线段叫做点到直线的距离 |
12.若(a-1)2+|b-2|=0,则(a-b)2016的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
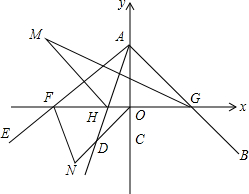 如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.
如图,平面直角坐标系中,∠BAC=45°,AC在y轴上,∠DAE=35°,AE,AB,AD分别交x轴于点F、G、H.在∠DAE旋转过程中,设AE交x轴于F,∠AGH的平分线与∠AHF的平分线交于点M,∠COF的平分线与∠OFE的平分线交于点N.下列两个结论:①∠N+∠M为定值;②∠N-∠M为定值.其中有且仅有一个是正确的,请你选出正确的结论,并求出其值.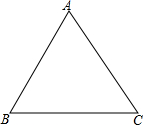 已知△ABC中,AB=AC=BC=3.请在图中用尺规作图画出△ABC的内切圆,保留作图痕迹,并求出内切圆的半径.
已知△ABC中,AB=AC=BC=3.请在图中用尺规作图画出△ABC的内切圆,保留作图痕迹,并求出内切圆的半径.