题目内容
18.已知二次函数y=kx2+2x-1与x轴有交点,则k的取值范围k≤-1.分析 根据抛物线与x轴有交点,可得相应方程有实数根,根据根的判别式,可得答案.
解答 解:由二次函数y=kx2+2x-1与x轴有交点,得
kx2+2x-1=0有实数根,
△=b2-4ac=4+4k≥0,
解得k≥-1,
故答案为:k≥-1.
点评 本题考查了了抛物线与x轴的交点,利用根的判别式得出不等式是解题关键.

练习册系列答案
相关题目
10.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2-2b2,则( )
| A. | △ABC是直角三角形,且∠A为直角 | B. | △ABC是直角三角形,且∠B为直角 | ||
| C. | △ABC是直角三角形,且∠C为直角 | D. | △ABC不是直角三角形 |
7.下列各组单项式中,不是同类项的是( )
| A. | 3x2y与-2yx2 | B. | 2ab2与-ba2 | C. | $\frac{xy}{3}$与5xy | D. | 23a与32a |
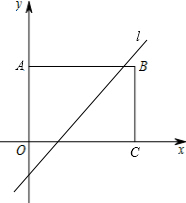 如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.
如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.