题目内容
4．在Rt△ABC中，∠C=90°，AC=3，BC=4，D为AB的中点，则CD=2.5．分析 根据勾股定理求出AB的长，根据直角三角形的性质计算即可．
解答 解：∵∠C=90°，AC=3，BC=4，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∵D为AB的中点，
∴CD=2.5，
故答案为：2.5．
点评 本题考查的是直角三角形的性质和勾股定理的应用，掌握直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC，AC=BC，且∠ACB=∠ADC=∠BEC=100°，求证：DE=AD+BE．
已知，如图，四边形ABCD中，AC=7，BD=8，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长=15．
12．有以下四种说法：
①过一点有且只有一条直线与已知直线垂直；
②过直线外一点有且只有一条直线与已知直线平行；
③平行于同一条直线的两条直线平行；
④垂直于同一条直线的两条直线垂直；
③直线外一点和直线上所有点的连线中，垂线段最短．
其中正确的有（ ）
①过一点有且只有一条直线与已知直线垂直；
②过直线外一点有且只有一条直线与已知直线平行；
③平行于同一条直线的两条直线平行；
④垂直于同一条直线的两条直线垂直；
③直线外一点和直线上所有点的连线中，垂线段最短．
其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
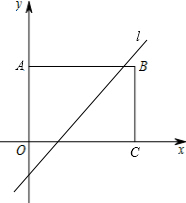如图，矩形OABC中，A、C分别是y轴、x轴上的点，且OA=3，OC=4，将矩形OABC沿直线l折叠，使A点与C点重合，则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$．
2．
如图，在△ABC中，AB=6，∠B=60°，以BC所在直线为x轴，以B点为原点建立直角坐标系，则点A的坐标是（ ）
如图，在△ABC中，AB=6，∠B=60°，以BC所在直线为x轴，以B点为原点建立直角坐标系，则点A的坐标是（ ）| A． | （3，3） | B． | （3$\sqrt{3}$，3） | C． | （3，$3\sqrt{3}$） | D． | （3$\sqrt{3}$，3$\sqrt{3}$） |