题目内容
14．
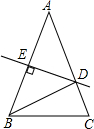如图，△ABC中，AB=AC，∠C=72°，AB的垂直平分线DE交AC于D，交AB于E，则∠BDC的度数为（ ）| A． | 36° | B． | 60° | C． | 72° | D． | 82° |
分析 先根据AB=AC，∠C的度数，再由垂直平分线的性质求出∠ABD的度数，再由三角形内角与外角的性质解答即可．
解答 解：∵AB=AC，∠C=72°，
∴∠ABC=∠C=72°，
∵DE垂直平分AB，
∴∠A=∠ABD=36°，
∴∠BDC=∠A+∠ABD=36°+36°=72°．
故选C．
点评 本题考查的是线段垂直平分线的性质及三角形内角和定理、等腰三角形的性质，解答此题的关键是熟知线段垂直平分线的性质，即线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，线段AB=8，M是线段AB的中点，N是线段AC的中点，C为线段AB上一点，且AC=3.2，求M，N两点间的距离．
2．下列四个命题中，正确的个数是（ ）
①经过三点一定可以画圆；
②任意一个三角形一定有一个外接圆；
③三角形的内心是三角形三条角平分线的交点；
④三角形的外心到三角形三个顶点的距离都相等；
⑤三角形的外心一定在三角形的外部．
①经过三点一定可以画圆；
②任意一个三角形一定有一个外接圆；
③三角形的内心是三角形三条角平分线的交点；
④三角形的外心到三角形三个顶点的距离都相等；
⑤三角形的外心一定在三角形的外部．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图，在平面直角坐标系中，O为原点，一次函数y1=x+m与反比例函数y2=$\frac{k}{x}$的图象相交于A（2，1），B（n，-2）两点，与x轴交于点C．
3．某校初三（1）班、（2）班各有49名学生，在一次数学测验中的成绩统计如表：
（1 ）九（1）班的小亮回家对妈妈说：“这次数学测验，全班平均80分，得70分的人最多，我得了87分，在班里可算上游了！”问小亮的成绩可以算作上游吗？请你进行简要分析：
（2）请你根据表中数据，对这两个班的测验情况进行简要分析，并提出教学建议．
| 班级 | 平均分（分） | 众数（分） | 中位数（分） | 方差（分2） |
| 九（1）班 | 80 | 70 | 88 | 234.1 |
| 九（2）班 | 80 | 70 | 80 | 37.2 |
（2）请你根据表中数据，对这两个班的测验情况进行简要分析，并提出教学建议．
4．
如图，线段EF的长为4，O是EF的中点，以OF为边长做正方形OABC，连接AE、CF交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°止，则点P运动的路径长为（ ）
如图，线段EF的长为4，O是EF的中点，以OF为边长做正方形OABC，连接AE、CF交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°止，则点P运动的路径长为（ ）| A． | $\frac{\sqrt{2}}{2}$π | B． | $\sqrt{2}$π | C． | 2π | D． | 2$\sqrt{2}$π |