题目内容
9. 如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2=$\frac{k}{x}$的图象相交于A(2,1),B(n,-2)两点,与x轴交于点C.
如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2=$\frac{k}{x}$的图象相交于A(2,1),B(n,-2)两点,与x轴交于点C.(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是-1<x<0或x>2时,有y1>y2.
分析 (1)将点A坐标代入反比例函数解析式中即可求出k值,从而得出反比例函数解析式,再将点B的坐标代入反比例函数解析式中即可求出n值,进而可得出点B的坐标,此题得解;
(2)观察两函数图象的上下位置关系,即可找出不等式的解集.
解答 解:(1)将A(2,1)代入y2=$\frac{k}{x}$,
1=$\frac{k}{2}$,解得:k=2,
∴反比例函数解析式为y2=$\frac{2}{x}$.
将B(n,-2)代入y2=$\frac{2}{x}$,
-2=$\frac{2}{n}$,解得:n=-1,
∴点B的坐标为(-1,-2).
(2)观察函数图象发现:当-1<x<0或x>2时,一次函数图象在反比例函数图象上方,
∴当x的取值范围是-1<x<0或x>2时,有y1>y2.
故答案为:-1<x<0或x>2.
点评 本题考查了反比例函数与一次函数的交点问题以及反比例函数图象上点的坐标特征,根据点的坐标利用反比例函数图象上点的坐标特征求出k值是解题的关键.

练习册系列答案
相关题目
19.如果A和B是一个直角三角形的两个锐角,那么( )
| A. | sinA=cosB | B. | sinA=sinB | C. | cosA=cosB | D. | sinB=cosB |
20.嫦娥三号于2015年12月14日晚21时11分11秒成功落月,着陆地点为虹湾,这是月球上最突丽的地标之一,它其实是一个直径达 260000m 的巨型陨石坑壁.虹湾的直径用科学记数法表示为( )m.
| A. | 2.6×105 | B. | 26×104 | C. | 2.6×104 | D. | 0.26×106 |
4.某种药品原价为49元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 49(1-x)2=49-25 | B. | 49(1-2x)=25 | C. | 49(1-x)2=25 | D. | 49(1-x2)=25 |
14.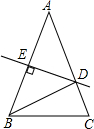 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )| A. | 36° | B. | 60° | C. | 72° | D. | 82° |
18.下列交通标志中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列式子正确的是( )
| A. | -2.1>-2.01 | B. | -2>0 | C. | $\frac{1}{3}$<$\frac{1}{4}$ | D. | -15<13 |