题目内容
3.已知关于x的方程mx2+(3m+1)x+3=0.(1)求证:不论m为任何实数,此方程总有实数根;
(2)若抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,试确定此抛物线的解析式;(温馨提示:整数点的横、纵坐标都为整数)
(3)若点P(x1,y1)与Q(x1+n,y2)在(2)中抛物线上 (点P、Q不重合),且y1=y2,求代数式4x12+12x1n+5n2+16n+2000的值.
分析 (1)分m=0与m≠0两种情况进行讨论即可;
(2)令y=0,则 mx2+(3m+1)x+3=0,求出x的值,再由抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数得出m的值,代入抛物线的解析式即可;
(3)把点P(x1,y1)与Q(x1+n,y2)代入抛物线的解析式,根据y1=y2可得出2x1=-n-4,代入代数式进行计算即可.
解答 解:(1)当m=0时,原方程化为x+3=0,
此时方程有实数根x=-3.
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2≥0,
∴此时方程有两个实数根.
综上,不论m为任何实数时,方程mx2+(3m+1)x+3=0总有实数根.
(2)∵令y=0,则 mx2+(3m+1)x+3=0.
解得x1=-3,x2=-$\frac{1}{m}$.
∵抛物线y=mx2+(3m+1)x+3与x轴交于两个不同的整数点,且m为正整数,
∴m=1.
∴抛物线的解析式为y=x2+4x+3.
(3)∵点P(x1,y1)与Q(x1+n,y2)在抛物线上,
∴y1=x12+4x1+3,y2=(x1+n)2+4(x1+n)+3,
∵y1=y2,
∴x12+4x1+3=(x1+n)2+4(x1+n)+3,
可得n(2x1+n+4)=0.
∵点P,Q不重合,
∴n≠0.
∴2x1=-n-4.
∴4x12+12x1n+5n2+16n+2000=(2x1)2+2x1-6n+5n2+16n+2000=(n+4)2+6n(-n-4)+5n2+16n+2000=2016.
点评 本题考查的是抛物线与x轴的交点,在解答(1)时要注意进行分类讨论,不要漏解.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
13.夏至将至,白沙电器超市销售每台进价分别为200元、170元的艾美特和格力两种品牌型号的电风扇,如表是近两周超市的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求艾美特和格力两种型号的电风扇的各自的销售单价;
(2)若白沙电器超市准备用不多于5700元的金额再采购这两种型号的电风扇共30台,求艾美特型号的电风扇最多能采购多少台?
(3)在(2)的条件下,白沙电器超市销售完这30台电风扇能否实现利润为1440元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 销售数量 | 艾美特型号 | 格力型号 | 销售收入 |
| 第一周 | 5台 | 4台 | 2090元 |
| 第二周 | 4台 | 8台 | 2680元 |
(1)求艾美特和格力两种型号的电风扇的各自的销售单价;
(2)若白沙电器超市准备用不多于5700元的金额再采购这两种型号的电风扇共30台,求艾美特型号的电风扇最多能采购多少台?
(3)在(2)的条件下,白沙电器超市销售完这30台电风扇能否实现利润为1440元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
 如图所示,一棵大树在一次强烈台风中于离地面5m处折断倒下,树顶落在离树根12m处,求大树在折断之前的高度.
如图所示,一棵大树在一次强烈台风中于离地面5m处折断倒下,树顶落在离树根12m处,求大树在折断之前的高度. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. 如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.已知BD:CD=3:2,点D到AB的距离是6,则BC的长是15.
如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.已知BD:CD=3:2,点D到AB的距离是6,则BC的长是15. 如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).
如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).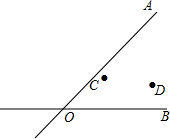 在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)
在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.) 如图,在△ABC中,CA=CB,点D在BC上,且AB=AD=DC,求∠C的度数.
如图,在△ABC中,CA=CB,点D在BC上,且AB=AD=DC,求∠C的度数.