题目内容
14.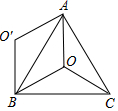 如图,△ABC是等边三角形,点O在△ABC内,点O′在△ABC外,若OA=OB=OC=O′A=O′B,则△OAB绕点O按顺时针方向旋转120°,能与△OCA重合,△OBC绕点B按逆时针方向旋转60°,能与△O′BA重合;△OAC绕点A按顺时针方向旋转60°,能与△O′AB重合.
如图,△ABC是等边三角形,点O在△ABC内,点O′在△ABC外,若OA=OB=OC=O′A=O′B,则△OAB绕点O按顺时针方向旋转120°,能与△OCA重合,△OBC绕点B按逆时针方向旋转60°,能与△O′BA重合;△OAC绕点A按顺时针方向旋转60°,能与△O′AB重合.
分析 根据等边三角形的性质得到AB=BC=AC,根据全等三角形的性质得到∠AOB=∠AOC,同理∠AOB=∠BOC,由周角的定义得到∠AOB=∠AOC=∠BOC=120°,根据等腰三角形的性质得到∠ABO=∠CBO=∠BAO=∠CAO=30°,于是得到结论.
解答 解:∵△ABC是等边三角形,
∴AB=BC=AC,
在△ABO与△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{BO=OC}\\{OA=OA}\end{array}\right.$,
∴△ABO≌△ACO,
∴∠AOB=∠AOC,
同理∠AOB=∠BOC,
∴∠AOB=∠AOC=∠BOC=120°,
∴∠ABO=∠CBO=∠BAO=∠CAO=30°,
∴将△OAB绕点O按顺时针方向旋转120°,能与△OCA重合;
△OBC绕点B按逆时针方向旋转60°,能与△O′BA重合;
△OAC绕点A按顺时针方向旋转60°,能与△O′AB重合.
故答案为:120,60,顺,60,△O′AB.
点评 本题考查了旋转的性质,等边三角形的性质,全等三角形的判定和性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
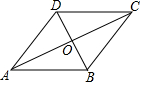 如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形.
如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形. 如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.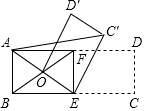 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长. 如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点.
如图,函数y=-2x与y=$\frac{k}{x}$的图象相交于A(m,2)、B两点.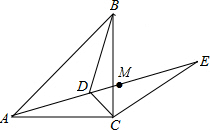 如图,已知∠ACB=90°,AC=BC,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知∠ACB=90°,AC=BC,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.