题目内容
2.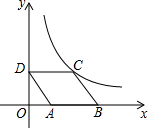 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).
分析 根据点A、B、D的坐标结合平行四边形的性质即可得出点C的坐标,由点C的坐标利用反比例函数图象上点的坐标特征即可得出反比例函数解析式,设点B′的坐标为(6,m),由点B′在反比例函数图象上即可求出m值,从而可找出点C′、D′的坐标,由点C′、D′的纵坐标利用反比例函数图象上点的坐标特征即可得出点E的坐标,此题得解.
解答 解:∵点A(2,0),B(6,0),D(0,3),四边形ABCD为平行四边形,
∴C(4,3).
∵反比例函数的图象经过点C,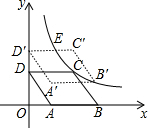
∴反比例函数解析式为y=$\frac{12}{x}$.
设点B′的坐标为(6,m),
∵点B′在反比例函数y=$\frac{12}{x}$的图象上,
∴6m=12,解得:m=2,
∴D′(0,5),C′(4,5).
∵C′D′与双曲线交于点E,
∴E($\frac{12}{5}$,5).
故答案为:($\frac{12}{5}$,5).
点评 本题考查了反比例函数图象上点的坐标特征、平行四边形的性质以及坐标与图形变化中的平移,根据平行四边形的性质找出点C的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数解析式是解题的关键.

练习册系列答案
相关题目
7.为宣传2022年北京-张家口冬季奥运会,小王在网上销售一种成本为20元/件的本届冬季奥运会宣传文化衫,销售过程中的其他各种费用(不再含文化衫成本)总计50(百元),有关销售量y(百件)与销售价格x(元/件)的相关信息如下:
(1)求销售这种文化衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
| 销售量y(百件) | y=-0.1x+8 | y=$\frac{120}{x}$ |
| 销售价格x(元/件) | 30≤x≤60 | 60<x≤80 |
(2)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?
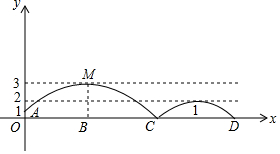 如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据:$\sqrt{3}$=$\frac{7}{4}$,$\sqrt{6}$=$\frac{5}{2}$)
如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据:$\sqrt{3}$=$\frac{7}{4}$,$\sqrt{6}$=$\frac{5}{2}$)