题目内容
20．
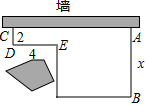用一段长为32m的篱芭绕过障碍物围成一个菜园，菜园一边靠墙．如图，已知CD=2m，DE=4m，设AB=x（m）（2＜x＜14），菜园面积为y（m2），请回答下列问题：（1）求y与x之间的函数关系式．
（2）当x取何值时，菜园面积最大，最大面积是多少．
分析 （1）先用含x的代数式表示出平行于墙的边长，再由矩形的面积公式就可以得出结论；
（2）利用二次函数的性质求出y的最大值，以及此时x的值即可．
解答 解：（1）y=2×4+x[32-x-（x-2）]=-2x2+34x+8；
（2）∵y=-2x2+34x+8=-2（x-$\frac{17}{2}$）2+610，
∴x=$\frac{17}{2}$m时，菜园面积最大，最大面积是610m2．
点评 此题主要考查了二次函数的应用，难度一般，应注意配方法求最大值在实际中的应用．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图，在△ABC中，∠ABC=45°，AD⊥BC于点D，点E在AD上，且DE=DC．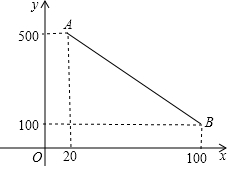
小明家买了一台充电式自动扫地机，每次完成充电后，在使用时扫地机会自动根据设定扫地时间，来确定扫地的速度（以使每次扫地结束时尽量把所储存的电量用完），如图是“设定扫地时间”与“扫地速度”之间的函数图象（线段AB），其中设定扫地时间为x分钟，扫地速度为y平方分米/分钟．
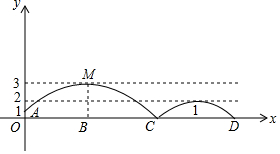如图，需在一面墙上绘制两个形状相同的抛物绒型图案，按照图中的直角坐标系，最高点M到横轴的距离是4米，到纵轴的距离是6米；纵轴上的点A到横轴的距离是1米，右侧抛物线的最大高度是左侧抛物线最大高度的一半．（结果保留整数或分数，参考数据：$\sqrt{3}$=$\frac{7}{4}$，$\sqrt{6}$=$\frac{5}{2}$）
如图，AD与BC相交，连接AB、CD，写出∠A、∠B、∠C、∠D之间的关系∠A+∠B=∠C+∠D．