题目内容
7.如图,正方形ABCD由16个边长为1的小正方形组成,形变后变成菱形A′B′C′D′,△AEF(E,F是小正方形的顶点)同时形变为△A′E′F.设这个菱形的“形变度”为k,对于△AEF与△A′E′F′的面积之比你有何猜想,当△AEF与△△A′E′F′的面积之比等于2:$\sqrt{3}$时,求A′C′的长.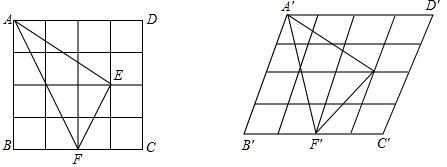
分析 先求出△AEF的面积,再根据面积关系求出∠A′B′C′=60°,证明△A′B′C′是等边三角形,得出A′C′=A′B′=4.
解答 解:如图所示: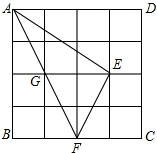
S△AEF=S△AGF+S△GEF=$\frac{1}{2}$GE•AB=$\frac{1}{2}$×2×4=4,
△AEF变成菱形A′B′C′D′时的△A′E′F′的面积,G′E′的长度没有变化,
A′到B′C′的距离变小了,A′B′的长度也没有变化,
而A′到B′C′的距离的大小取决于∠A′B′C′,
设∠A′B′C′=α,
过点A′作A′H′⊥B′C′,垂足为H′,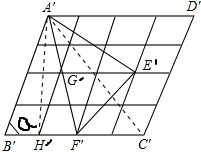
则A′H′=A′B′sinα=4sinα,
∴S△A′E′F′=$\frac{1}{2}$G′E′•A′H′=$\frac{1}{2}$×2×4sinα,
∴S△AEF:S△A′E′F′=4:4sinα=2:$\sqrt{3}$,sinα=$\frac{\sqrt{3}}{2}$,
∴α=60°,
又∵A′B′=B′C′,
∴△A′B′C′是等边三角形,
∴A′C′=A′B′=4.
点评 本题考查了正方形的性质、菱形的性质、等边三角形的判定与性质以及三角形面积的计算;根据面积关系求出∠A′B′C′,证明等边三角形是解决问题的关键.

练习册系列答案
相关题目
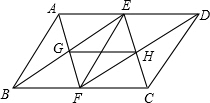 如图:E、F分别是?ABCD的对边AD、BC的中点,AF、BE交于点G,EC与DF交于H.
如图:E、F分别是?ABCD的对边AD、BC的中点,AF、BE交于点G,EC与DF交于H.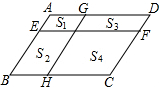 如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( )
如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( )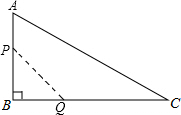 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.