题目内容
16.关于x的方程:-$\frac{3}{2}$(x+m)=$\frac{3x+25}{3}$+1的解是正数,那么m的取值范围是?分析 首先去分母、去括号、移项、合并同类项、系数化成1,求得x的值,然后根据方程的解是正数得到关于m的不等式,从而求解.
解答 解:去分母,得:-9(x+m)=2(3x+25),
去括号,得:-9x-9m=6x+50,
移项得-9x-6x=50+9m,
合并同类项-15x=50+9m,
系数化成1得x=-$\frac{50+9m}{15}$,
根据题意得:-$\frac{50+9m}{15}$>0,
解得:m<-$\frac{50}{9}$.
点评 本题是一个方程与不等式的综合题目.解关于x的方程是本题的一个难点.

练习册系列答案
相关题目
6.计算4$\sqrt{6{x}^{3}}$÷2$\sqrt{\frac{x}{3}}$的结果为( )
| A. | 2$\sqrt{2}x$ | B. | $\frac{2x}{3}$ | C. | 6$\sqrt{2}x$ | D. | $\frac{2\sqrt{2}}{3}$x |
1.给出下列各数:①1+$\sqrt{5}$②1-$\sqrt{5}$③-1④$\sqrt{5}$,其中是方程x2-(1+$\sqrt{5}$)x+$\sqrt{5}$=0的解的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
11.已知$\frac{1}{x}-\frac{1}{y}=2$,则$\frac{2}{y^2}+\frac{2y-4x}{{{x^2}y}}$的值是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 8 | D. | $\frac{1}{8}$ |
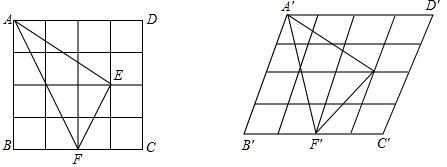
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高