题目内容
15.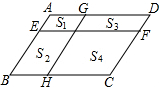 如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( )
如图,EF和GH将?ABCD分成四个小平行四边形,设面积分别为S1=1,S2=3,S3=4,那么S4等于( )| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
分析 首先设直线AD到EF的距离为h1,EF到BC的距离为h2,根据平行四边形的性质知,S1=BH•h1,S4=CH•h2,S2=BH•h2,S3=CH•h1,即可证得S1S4=S2S3,继而求得答案.
解答 解:设直线AD到EF的距离为h1,EF到BC的距离为h2,
根据平行四边形的性质知,S1=BH•h1,S4=CH•h2,S2=BH•h2,S3=CH•h1,
∴S1S4=BH•CH•h1•h2,S2S3=BH•CH•h1•h2,
∴S1S4=S2S3,
∵S1=1,S2=3,S3=4,
∴S4=12.
故选D.
点评 此题考查了平行四边形的性质.注意证得S1S4=S2S3是解此题的关键.

练习册系列答案
相关题目
6.计算4$\sqrt{6{x}^{3}}$÷2$\sqrt{\frac{x}{3}}$的结果为( )
| A. | 2$\sqrt{2}x$ | B. | $\frac{2x}{3}$ | C. | 6$\sqrt{2}x$ | D. | $\frac{2\sqrt{2}}{3}$x |
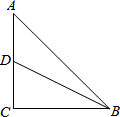 在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则:
在Rt△ABC中,∠C=90°,AC=BC=4,D是AC中点,则: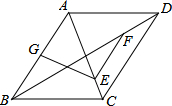 如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.
如图,在平行四边形ABCD中,BD=2AD,点E、F、G分别为OC、OD、AB的中点,求证:EF=EG.