题目内容
如图，已知：?ABCD中，CE⊥AD，CF⊥AB，∠B=50°，求∠ECF的度数．考点：平行四边形的性质
专题：
分析：由∠B的度数可求出∠A的度数，再根据垂直的性质和四边形的内角和为360°，即可求出∠ECF的度数．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠B+∠A=180°，
∵∠B=50°，
∴∠A=130°，
∵CE⊥AD，CF⊥AB，
∴∠AFC∠AEC=90°，
∴∠ECF=360°-2×90°-130°=50°．
∴AD∥BC，
∴∠B+∠A=180°，
∵∠B=50°，
∴∠A=130°，
∵CE⊥AD，CF⊥AB，
∴∠AFC∠AEC=90°，
∴∠ECF=360°-2×90°-130°=50°．
点评：本题考查了平行四边形的性质、垂直的性质以及四边形内角和定理的运用，是中考常见题型．
练习册系列答案
相关题目
将二次函数y=x2-2x+3化为y=（x+m）2+h的形式，结果为（ ）
| A、y=（x-1）2+4 |
| B、y=（x+1）2+4 |
| C、y=（x-1）2+2 |
| D、y=（x+1）2+2 |
△ABC≌△A1B1C1，其中△ABC三边为x、6、3，另一个△A1B1C1 三边为3、y、8．那么2x+y（ ）
| A、8 | B、6 | C、22 | D、24 |
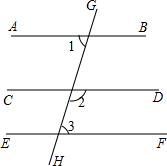如图，直线AB、CD、EF被直线GH所截，∠1=70°，∠2=110°，∠2+∠3=180°，试说明：（1）EF∥AB．（2）CD∥AB（ 补全横线及括号的内容 ）
如图，?ABCD中，AB⊥AC，AB=1，BC=
如图，DE∥BC，CG=GB，∠1=∠2，求证：△DGE是等腰三角形．
如图，已知AB为⊙O的直径，PB与⊙O相切于点B，线段OP与弦BC垂直并相交于点D，OP与弧BC相交于点E，连接AC．