题目内容
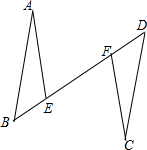如图，AB∥CD，AB=CD，点B、E、F、D在一条直线上，∠A=∠C，求证：BF=DE．考点：全等三角形的判定与性质
专题：证明题
分析：利用平行可得∠B=∠D，结合∠A=∠C和AB=CD，可证明△ABE≌△CDF，可得结论．
解答：证明：∵AB∥CD，
∴∠B=∠D，
在△ABE和△CDF中
∴△ABE≌△CDF（ASA），
∴BF=DE．
∴∠B=∠D，
在△ABE和△CDF中
|
∴△ABE≌△CDF（ASA），
∴BF=DE．
点评：本题主要考查三角形全等的判定和性质，正确掌握三角形全等的判定方法是解题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
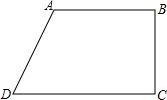如图，在梯形ABCD中，∠B=∠C=90°，AB∥CD；AB=BC=3cm，CD=4cm，有一动点P从A点出发沿A→B→C→D移动，P点在AB边和BC边上移动的速度为1cm/s，在CD边上移动时速度为2cm/s；若运动时间为t（s），运动过程中△PBD的面积为3cm2，求t的值．
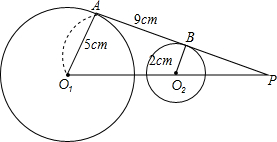如图所示，直线AB为⊙O1与⊙O2的一条外公切线，O1A=5cm，AB=9cm，O2B=2cm，求：已知二次函数y=x2-6x+m的图象过A（-3，a），B（0，b），C（5，c）三点，则a、b、c的大小关系是（ ）
| A、c＞b＞a |
| B、a＞b＞c |
| C、a＞c＞b |
| D、c＞a＞b |
将Rt△ABC的各边都扩大2倍，则锐角B的余弦值（ ）
| A、不变 | B、扩大2倍 |
| C、是原来的0.5倍 | D、不能确定 |