题目内容
一个周长为40cm的等腰三角形,腰长为x,底边长为y,求:
①求y与x的函数关系式;
②求自变量x的取值范围.
①求y与x的函数关系式;
②求自变量x的取值范围.
考点:函数关系式,函数自变量的取值范围
专题:
分析:①根据:底边长+两腰长=周长,建立等量关系,变形即可;
②根据三角形两边之和大于第三边及周长的限制,确定自变量的取值范围.
②根据三角形两边之和大于第三边及周长的限制,确定自变量的取值范围.
解答:解:①依题意得2x+y=40,
即y=-2x+40;
②根据三角形的三边关系得:
解得:10<x<20.
即y=-2x+40;
②根据三角形的三边关系得:
|
解得:10<x<20.
点评:本题考查了等腰三角形三边关系的性质,三角形三边关系定理.

练习册系列答案
相关题目
下列方程有两个不相等的实数根的是( )
| A、x2+2=0 |
| B、x2-2x=-1 |
| C、x2+2x+5=0 |
| D、x2-3x+1=0 |
抛物线y=-x2+1的对称轴是( )
| A、直线x=1 |
| B、直线x=0 |
| C、直线x=-1 |
| D、直线y=0 |
笔尖在纸上快速滑动写出一个又一个字,用数学知识解释为( )
| A、点动成线 | B、线动成面 |
| C、面动成体 | D、以上答案都不对 |
已知直线y=2x与直线y=kx+5互相平行,则k的值为( )
| A、k=-2 | B、k=2 |
| C、k=±2 | D、无法确定k的值 |
如果|a|=a,则( )
| A、a是非正数 |
| B、a是非负数 |
| C、a是非正整数 |
| D、a是非负整数 |
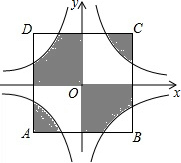 边长为2的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=
边长为2的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=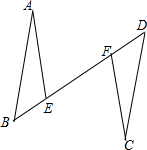 如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE.
如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE.