题目内容
已经抛物线y=x2-3x-4与x轴的交点为A、B,与y轴的交点为C
(1)求A、B、C三点的坐标;
(2)若该抛物线的顶点为P,求△PAB的面积.
(1)求A、B、C三点的坐标;
(2)若该抛物线的顶点为P,求△PAB的面积.
考点:抛物线与x轴的交点
专题:
分析:(1)在y=x2-3x-4中,令y=0,即可求得与x轴的交点的横坐标,令x=0,即可求得与y轴的交点的纵坐标;
(2)首先求得顶点坐标,利用三角形的面积公式即可求解.
(2)首先求得顶点坐标,利用三角形的面积公式即可求解.
解答:解:(1)在y=x2-3x-4中,令y=0,则x2-3x-4=0,
解得:x1=-1,x2=4,
则A和B的坐标分别是(-1,0)和(4,0).
在y=x2-3x-4中,令x=0,则y=-4,
则C的坐标是(0,-4).
(2)顶点的横坐标是x=-
=
,
则纵坐标是(
)2-3×
-4=-
.
则S△PAB=
×5×
=
.
解得:x1=-1,x2=4,
则A和B的坐标分别是(-1,0)和(4,0).
在y=x2-3x-4中,令x=0,则y=-4,
则C的坐标是(0,-4).
(2)顶点的横坐标是x=-
| -3 |
| 2 |
| 3 |
| 2 |
则纵坐标是(
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 4 |
则S△PAB=
| 1 |
| 2 |
| 25 |
| 4 |
| 125 |
| 8 |
点评:本题考查了二次函数与x、y轴的交点的求解方法,以及顶点的确定方法,是一个基础题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
如果|a|=a,则( )
| A、a是非正数 |
| B、a是非负数 |
| C、a是非正整数 |
| D、a是非负整数 |
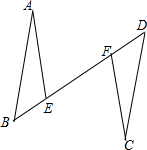 如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE.
如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE. 如图,⊙O中,弦AB、CD相交于点E,过点B作BF∥CD交AD延长线于点F.
如图,⊙O中,弦AB、CD相交于点E,过点B作BF∥CD交AD延长线于点F.  如图,小明从点A出发沿直线向前走10m,向左转30°,然后继续向前走10m,再向左转30°,他以同样的方法继续走下去,当他第一次回到出发地A点时,一共走了
如图,小明从点A出发沿直线向前走10m,向左转30°,然后继续向前走10m,再向左转30°,他以同样的方法继续走下去,当他第一次回到出发地A点时,一共走了