题目内容
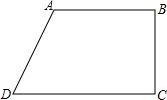 如图,在梯形ABCD中,∠B=∠C=90°,AB∥CD;AB=BC=3cm,CD=4cm,有一动点P从A点出发沿A→B→C→D移动,P点在AB边和BC边上移动的速度为1cm/s,在CD边上移动时速度为2cm/s;若运动时间为t(s),运动过程中△PBD的面积为3cm2,求t的值.
如图,在梯形ABCD中,∠B=∠C=90°,AB∥CD;AB=BC=3cm,CD=4cm,有一动点P从A点出发沿A→B→C→D移动,P点在AB边和BC边上移动的速度为1cm/s,在CD边上移动时速度为2cm/s;若运动时间为t(s),运动过程中△PBD的面积为3cm2,求t的值.考点:梯形
专题:动点型
分析:分三种情况讨论列出关于△PBD的面积的含有t的方程,解方程即可求得.
解答: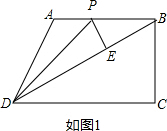 解:如图1,作PE⊥BD于E,
解:如图1,作PE⊥BD于E,
∵AB=BC=3cm,CD=4cm,
∴BD=
=5cm,
当P在AB上时,PB=3-t,
设P到BD的距离是xcm,
∵AB∥CD,
∴∠PBE=∠BDC,
∵∠PEB=∠C=90°,
∴△PEB∽DCB,
=
,
∴x=
,
∴
×5×
=3,
∴t=1;
如图2,当P在BC上时BP=t-3,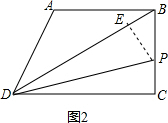
∵∠PBE=∠DBC,∠PEB=∠C,
∴△PBE∽△DBC,
∴
=
,
∴
=
,
∴x=
,
∴
×5×
=3,
∴t=4.5;
如图3,当p在DC上时PD=10-2t,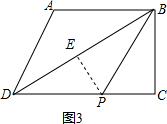
∵∠PDE=∠BDC,∠PED=∠C=90°,
∴△PED∽△BCD,
∴
=
,
即
=
,
∴x=
,
∴
×5×
=3,
∴t=4;
综上所述,当t的值为1 或4.5或4时△PBD的面积为3
 解:如图1,作PE⊥BD于E,
解:如图1,作PE⊥BD于E,∵AB=BC=3cm,CD=4cm,
∴BD=
| BC2+DC2 |
当P在AB上时,PB=3-t,
设P到BD的距离是xcm,
∵AB∥CD,
∴∠PBE=∠BDC,
∵∠PEB=∠C=90°,
∴△PEB∽DCB,
| PB |
| BD |
| x |
| BC |
∴x=
| 3(3-t) |
| 5 |
∴
| 1 |
| 2 |
| 3(3-t) |
| 5 |
∴t=1;
如图2,当P在BC上时BP=t-3,

∵∠PBE=∠DBC,∠PEB=∠C,
∴△PBE∽△DBC,
∴
| BP |
| PE |
| BD |
| DC |
∴
| BP |
| x |
| 5 |
| 4 |
∴x=
| 4(t-3) |
| 5 |
∴
| 1 |
| 2 |
| 4(t-3) |
| 5 |
∴t=4.5;
如图3,当p在DC上时PD=10-2t,

∵∠PDE=∠BDC,∠PED=∠C=90°,
∴△PED∽△BCD,
∴
| PD |
| BD |
| PE |
| BC |
即
| 10-2t |
| 5 |
| x |
| 3 |
∴x=
| 3(10-2t) |
| 5 |
∴
| 1 |
| 2 |
| 3(10-2t) |
| 5 |
∴t=4;
综上所述,当t的值为1 或4.5或4时△PBD的面积为3
点评:本题考查了梯形的性质,三角形相似的判定和性质,三角形的面积公式的应用,数形结合是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
比较a与3a的大小,正确的是( )
| A、3a>a | B、3a=a |
| C、3a<a | D、上述情况都可能 |
下列方程有两个不相等的实数根的是( )
| A、x2+2=0 |
| B、x2-2x=-1 |
| C、x2+2x+5=0 |
| D、x2-3x+1=0 |
抛物线y=-x2+1的对称轴是( )
| A、直线x=1 |
| B、直线x=0 |
| C、直线x=-1 |
| D、直线y=0 |

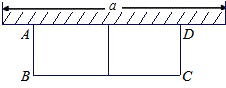 如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.
如图,有长为30米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米).设花圃的一边AB长为x米,面积为y平方米.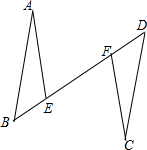 如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE.
如图,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C,求证:BF=DE.