题目内容
 如图,在平行四边形ABCD中,AC,BD相交于点O,过点O作直线与AB,CD相交于E,F,与DA,BC的延长线相交于M,N,求证:
如图,在平行四边形ABCD中,AC,BD相交于点O,过点O作直线与AB,CD相交于E,F,与DA,BC的延长线相交于M,N,求证:(1)BE=DF;
(2)OM=ON.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用平行四边形的性质得出∠ABO=∠FDO,进而利用ASA得出△BOE≌△DOF即可得出答案;
(2)利用平行四边形的性质得出∠M=∠N,进而利用AAS得出△AOM≌△CON即可得出答案.
(2)利用平行四边形的性质得出∠M=∠N,进而利用AAS得出△AOM≌△CON即可得出答案.
解答:证明:(1)∵在平行四边形ABCD中,AC,BD相交于点O,
∴BO=DO,AB∥CD,
∴∠ABO=∠FDO,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF;
(2))∵在平行四边形ABCD中,AC,BD相交于点O,
∴AO=CO,AD∥CB,
∴∠M=∠N,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS),
∴MO=NO.
∴BO=DO,AB∥CD,
∴∠ABO=∠FDO,
在△BOE和△DOF中,
|
∴△BOE≌△DOF(ASA),
∴BE=DF;
(2))∵在平行四边形ABCD中,AC,BD相交于点O,
∴AO=CO,AD∥CB,
∴∠M=∠N,
在△AOM和△CON中,
|
∴△AOM≌△CON(AAS),
∴MO=NO.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

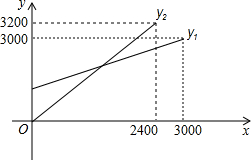 某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?