题目内容
抛物线y=x2+bx+c和x轴交于点A、B,顶点为C,且△ABC的面积为1,求b2-4c的值.
考点:抛物线与x轴的交点
专题:计算题,数形结合
分析:设抛物线y=x2+bx+c和x轴交于点A、B的横坐标分别是x1、x2.根据根与系数的关系的关系求得AB=
.由抛物线的解析式求得顶点C的坐标是(-
,
).然后根据三角形的面积公式得到:
×
×|
|=1,整理后为:(b2-4c)3=43.
| b2-4c |
| b |
| 2 |
| 4c-b2 |
| 4 |
| 1 |
| 2 |
| b2-4c |
| 4c-b2 |
| 4 |
解答:解:设抛物线y=x2+bx+c和x轴交于点A、B的横坐标分别是x1、x2.
则x1+x2=-b,x1•x2=c,
∴AB=|x2-x2|=
=
.
又∵抛物线y=x2+bx+c的顶点为C,
∴C(-
,
).
∵△ABC的面积为1,
∴
×
×|
|=1,
整理,得
(b2-4c)3=43,
解得,b2-4c=4.
答:b2-4c的值是4.
则x1+x2=-b,x1•x2=c,
∴AB=|x2-x2|=
| (x1+x2)2-4x1x2 |
| b2-4c |
又∵抛物线y=x2+bx+c的顶点为C,
∴C(-
| b |
| 2 |
| 4c-b2 |
| 4 |
∵△ABC的面积为1,
∴
| 1 |
| 2 |
| b2-4c |
| 4c-b2 |
| 4 |
整理,得
(b2-4c)3=43,
解得,b2-4c=4.
答:b2-4c的值是4.
点评:本题考查了抛物线与x轴的交点.此题的难点是根据抛物线的解析式推知AB=
.另外,在解
×
×|
|=1时,注意把(b2-4c)看成一个整体来解答.
| b2-4c |
| 1 |
| 2 |
| b2-4c |
| 4c-b2 |
| 4 |

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,函数y1=
如图,函数y1=| k1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、-1<x<0或x>1 |
| D、x<-1或0<x<1 |
 如图,在平行四边形ABCD中,AC,BD相交于点O,过点O作直线与AB,CD相交于E,F,与DA,BC的延长线相交于M,N,求证:
如图,在平行四边形ABCD中,AC,BD相交于点O,过点O作直线与AB,CD相交于E,F,与DA,BC的延长线相交于M,N,求证: 已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<
已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<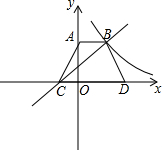 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数