题目内容
5.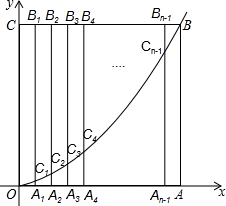 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
分析 根据题意表示出OA5,B5A5的长,由B5C5=3C5A5确定点C5的坐标,代入解析式计算得到答案.
解答 解:∵正方形OABC的边长为n,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,
∴OA5=$\frac{5}{n}$•n=5,A5B5=n,
∵B5C5=3C5A5,
∴C5(5,$\frac{n}{4}$),
∵点C5在y=$\frac{1}{n}$x2(x≥0)上,
∴$\frac{n}{4}$=$\frac{1}{n}$×52,
解得n=10.
故答案为:10.
点评 本题考查的是二次函数图象上点的特征和正方形的性质,根据正方形的性质表示出点C5的坐标是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
16.计算2.7×10-8-2.6×10-8,结果用科学记数法表示为( )
| A. | 0.1×10-8 | B. | 0.1×10-7 | C. | 1×10-8 | D. | 1×10-9 |
20. 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,直线OA过点(4,3),则tanα=( )
如图,直线OA过点(4,3),则tanα=( )
 如图,直线OA过点(4,3),则tanα=( )
如图,直线OA过点(4,3),则tanα=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
14. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )
 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )| A. | 4 | B. | 2 | C. | 6 | D. | 2$\sqrt{3}$ |
15. 如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )
如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )
 如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )
如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点. 如图,一正方体包装箱沿斜面坡角为30°的电梯上行,已知正方体包装箱的棱长为2米,电梯AB长为16米,当正方体包装箱的一个顶点到达电梯上端B时,求另一顶点C离地面的高度.(参考数据:$\sqrt{3}$≈1.73)
如图,一正方体包装箱沿斜面坡角为30°的电梯上行,已知正方体包装箱的棱长为2米,电梯AB长为16米,当正方体包装箱的一个顶点到达电梯上端B时,求另一顶点C离地面的高度.(参考数据:$\sqrt{3}$≈1.73)