题目内容
13. 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
分析 (1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(-1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而可求得a=-1,b=2;
(2)过D点作DE∥BC交抛物线y=-x2+2x+3于E点,由△BCD与△BCE是同底等高的三角形可知S△BCD=S△BCE,设直线DE的解析式为y=-x+b,将点D的坐标代入可求得直线DE的解析式,然后与抛物线的解析式联立可求得点E的坐标;
(3)由两点间的而距离公式可知:BC=3$\sqrt{2}$,CD=$\sqrt{2}$,设M(x,y),则MN=y=-x2+2x+3,BN=3-x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
解答 解:(1)∵将x=0代入得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1.
∴A(-1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(-1,0),B(3,0)代入y=ax2+bx+3得:$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$.
∴抛物线解析式为y=-x2+2x+3.
(2)∵将x=1代入抛物线的解析式得:y=-1+2+3=4,
∴D(1,4).
如图1,过D点作DE∥BC交抛物线y=-x2+2x+3于E点.
设直线DE的解析式为y=-x+b,
将点D的坐标代入得:-1+b=4,解得:b=5,则直线DE的解析式为y=-x+5.
将y=-x+5与y=-x2+2x+3联立得:$\left\{\begin{array}{l}{y=-x+5}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=3}\end{array}\right.$.
∴E(2,3).
(3)存在.
由两点间的而距离公式可知:BC=$\sqrt{{3}^{2}+{3}^{2}}$3$\sqrt{2}$,CD=$\sqrt{(1-0)^{2}+(4-3)^{\;}}$=$\sqrt{2}$.
设M(x,y),则MN=y=-x2+2x+3,BN=3-x.
①如图2所示:
∵当△BMN∽△DBC时,$\frac{BN}{NM}=\frac{CD}{BC}=\frac{1}{3}$,
∴$\frac{3-x}{-{x}^{2}+2x+3}=\frac{1}{3}$.
解得:x1=2,x2=3(舍去).
∵当x=2时,y=3,
∴M(2,3).
②如图3所示:
∵当△BMN∽△BDC时,$\frac{MN}{BN}=\frac{DC}{BC}=\frac{1}{3}$,
∴$\frac{-{x}^{2}+2x+3}{3-x}=\frac{1}{3}$.
解得:x1=-$\frac{2}{3}$,x2=3(舍去).
当x=-$\frac{2}{3}$时,y=$\frac{11}{9}$,
∴M(-$\frac{2}{3}$,$\frac{11}{9}$)
综上,存在点M(2,3)或(-$\frac{2}{3}$,$\frac{11}{9}$),使△BMN与△BCD相似.
点评 本题主要考查的是二次函数的综合应用,本题主要涉及了待定系数法求一次函数、二次函数的解析式、一次函数与二次函数图象的交点、相似三角形的性质和判定等知识点,依据相似三角形的性质列出关于x的方程是解题的关键.

 阅读快车系列答案
阅读快车系列答案 如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )| A. | 0 | B. | 2$\sqrt{5}$ | C. | 4-2$\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )
如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )| A. | 30米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | (30+30$\sqrt{3}$)米 |
 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD. 如图,E是正方形ABCD对角线延长线上一点,连接DE,作E作DE的垂线CB和BA的延长线分别交于F和G,判断△GDF的形状并证明你的结论.
如图,E是正方形ABCD对角线延长线上一点,连接DE,作E作DE的垂线CB和BA的延长线分别交于F和G,判断△GDF的形状并证明你的结论.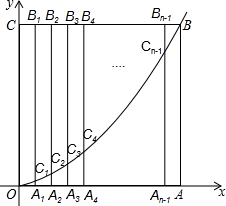 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10. 如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形.
如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形.