题目内容
14. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,BE=4,则AD的长是( )| A. | 4 | B. | 2 | C. | 6 | D. | 2$\sqrt{3}$ |
分析 由AB的垂直平分线DE交AC于E,得到AE=BE=4,根据三角形的内角和和对顶角的性质得到∠AED=∠CEF=60°,求得∠A=30°,于是得到结论.
解答 解:∵AB的垂直平分线DE交AC于E,
∴AE=BE=4,
∵∠ACB=90°,∠F=30°,
∴∠AED=∠CEF=60°,
∴∠A=30°,
∴AD=$\frac{\sqrt{3}}{2}$AE=2$\sqrt{3}$,
故选D.
点评 此题考查了线段垂直平分线的性质以及含30°的直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )
如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )
 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )
如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )| A. | 30米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | (30+30$\sqrt{3}$)米 |
 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.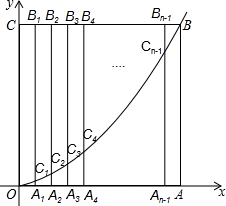 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10. 如图,等边△ABC的边长为4,AD是BC边上的中线,M是AD上的动点,E是AC边上点,若AE=1,EM+CM的最小值为$\sqrt{13}$.
如图,等边△ABC的边长为4,AD是BC边上的中线,M是AD上的动点,E是AC边上点,若AE=1,EM+CM的最小值为$\sqrt{13}$. 如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形.
如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形. 如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:AB=CD.
如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:AB=CD.