题目内容
15. 如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )
如图,在正方形ABCD中,△BCE是等边三角形,连接BD交CE于点M,若AB=$\sqrt{3}$,则EM的长为( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
分析 作MN⊥BC于N,则∠MNC=∠MNB=90°,由正方形和等边三角形的性质得出EC=BC=AB=$\sqrt{3}$,∠CBD=45°,∠MCN=60°,得出△BMN是等腰直角三角形,∠CMN=30°,因此BN=MN,设CN=x,则CM=2CN=2x,BN=MN=$\sqrt{3}$x,得出BC=$\sqrt{3}$x+x=$\sqrt{3}$,解方程求出CM,即可得出EM的长.
解答 解:作MN⊥BC于N,如图所示: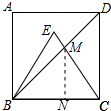
则∠MNC=∠MNB=90°,
∵四边形ABCD是正方形,△BCE是等边三角形,
∴EC=BC=AB=$\sqrt{3}$,∠CBD=45°,∠MCN=60°,
∴△BMN是等腰直角三角形,∠CMN=30°,
∴BN=MN,
设CN=x,则CM=2CN=2x,BN=MN=$\sqrt{3}$x,
∴BC=$\sqrt{3}$x+x=$\sqrt{3}$,
解得:x=$\frac{3-\sqrt{3}}{2}$,
∴CM=3-$\sqrt{3}$,
∴EM=CE-CM=$\sqrt{3}$-(3-$\sqrt{3}$)=2$\sqrt{3}$-3.
故选:B.
点评 本题考查了正方形的性质、等边三角形的性质、等腰直角三角形的判定与性质、含30°角的直角三角形的性质、勾股定理等知识;熟练掌握正方形和等边三角形的性质,通过设未知数得出方程是解决问题的关键.

练习册系列答案
相关题目
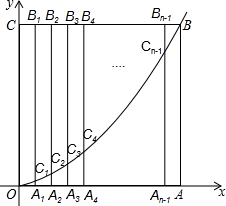 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10. 如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形.
如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形. AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$.
AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$. 如图,一个正多边形的半径为$\sqrt{2}$,边心距为1,求该正多边形的中心角、边长、内角、周长和面积.
如图,一个正多边形的半径为$\sqrt{2}$,边心距为1,求该正多边形的中心角、边长、内角、周长和面积.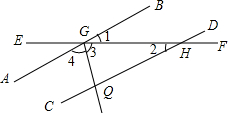 如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数.
如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数. 如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:AB=CD.
如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE.求证:AB=CD. 如图,AB∥CD,∠ECD=140°,∠FEC=65°,求∠BAF的度数.
如图,AB∥CD,∠ECD=140°,∠FEC=65°,求∠BAF的度数.