题目内容
4.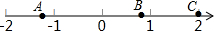 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
分析 根据数轴两点间的距离公式得到m-2=-$\sqrt{2}$,然后解方程即可得到m的值.
解答 解:由题意得m-2=-$\sqrt{2}$,
∴m=2-$\sqrt{2}$,即点B所表示的数为2-$\sqrt{2}$.
点评 本题考查了实数与数轴:实数与数轴上的点是一一对应关系;任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
16.若(x+4)(x-5)=x2+mx+n,则m+n=( )
| A. | 21 | B. | -21 | C. | 19 | D. | -19 |
14.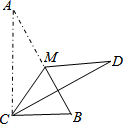 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
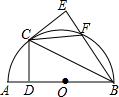 如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE. 已知△ABC,求作:AC边上的高.
已知△ABC,求作:AC边上的高.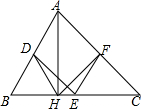 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.