题目内容
14.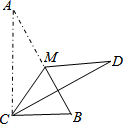 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
分析 首先设CD交AB于点E,根据折叠的性质可知,折叠前后的两个三角形全等,则∠D=∠A,∠MCD=∠MCA,再由直角三角形斜边中线的性质可得出∠MCD=∠D,从而求得∠A的度数,也就能得出tanA的值.
解答 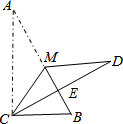 解:设CD交AB于点E,
解:设CD交AB于点E,
∵CM是直角△ABC的中线,
∴CM=AM=MB=$\frac{1}{2}$AB,
∴∠A=∠ACM,由折叠的性质可得:∠A=∠D,∠MCD=∠MCA,AM=DM,
∴MC=MD,∠A=∠ACM=∠MCD,
∵AB⊥CD,
∴∠CMB=∠DMB,∠CEB=∠MED=90°,
∵∠B+∠A=90°,∠B+∠ECB=90°,
∴∠A=∠ECB,
∴∠A=∠ACM=∠MCE=∠ECB,
∴∠A=$\frac{1}{3}$∠ACB=30°,
∴tanA=tan30°=$\frac{\sqrt{3}}{3}$.
故选A.
点评 此题考查了折叠的性质以及等腰三角形的判定与性质.注意掌握折叠前后图形的对应关系是关键.

练习册系列答案
相关题目
9.下列说法中,属于真命题的是( )
| A. | 垂线最短 | |
| B. | 两直线相交,邻补角相等 | |
| C. | 相等的角一定是对顶角 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
3.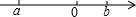 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
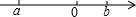 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )| A. | 2a+b | B. | 2a-b | C. | -2a+b | D. | b |
4.下列命题中逆命题是真命题的是( )
| A. | 对顶角相等 | |
| B. | 若两个角都是45°,那么这两个角相等 | |
| C. | 全等三角形的对应角相等 | |
| D. | 两直线平行,同位角相等 |
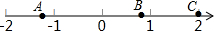 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.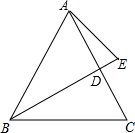 在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.
在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.