题目内容
18.(1)不改变分式的值,使分式$\frac{x-\frac{1}{5}{y}^{2}}{\frac{1}{2}x+{y}^{2}}$的分子与分母的最高次项的系数是整数;(2)不改变分式的值,使分式$\frac{x-{y}^{2}}{{x}^{3}+{y}^{2}}$的分子与分母的最高次项的系数是正数.
(3)当x满足什么条件时,分式$\frac{2-3x}{4{x}^{2}+1}$的值 ①等于0?②小于0?
分析 (1)根据分式的性质:分式的分子分母都乘以或除以同一个不为零的数,分式的值不变,可得答案;
(2)根据分式的分子、分母、分式改变其中任意两个的符号,分式的值不变,可得答案;
(3)根据解分式方程,可得答案;根据解不等式,可得答案.
解答 解:(1)原式=$\frac{10x-2{y}^{2}}{5x+10{y}^{2}}$;
(2)原式=-$\frac{{y}^{2}-x}{{x}^{3}+{y}^{2}}$;
(3)①$\frac{2-3x}{4{x}^{2}+1}$=0得2-3x=0,
解得x=$\frac{2}{3}$;
②$\frac{2-3x}{4{x}^{2}+1}$<0,得2-3x<0,
解得x>$\frac{2}{3}$.
点评 本题考查了分式的性质,分式的分子分母都乘以(或除以)同一个不为零的数,分式的值不变;分式的分子、分母、分式改变其中任意两个的符号,分式的值不变.

练习册系列答案
相关题目
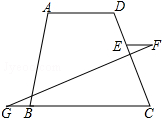 已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?
已知∠F=∠G,∠FEC+∠ADC=180°,试判断AD∥BC吗?为什么?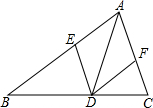 如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.
如图,已知AD平分∠BAC,要使△ADE≌△ADF,只需再添加一个条件就可以了,你选择的条件是AE=AF,理由是SAS.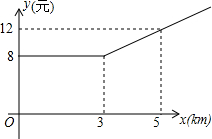 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请你根据图象解答下面的问题:
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请你根据图象解答下面的问题: