题目内容
11. 在平面直角坐标系中,点 A(-2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
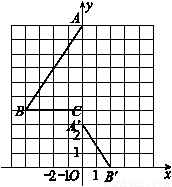
在平面直角坐标系中,点 A(-2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).
分析 (1)如图1中,首先判断△AD′C是直角三角形,再根据AC=2CD′推出∠CAD′=30°由此即可解决问题.
(2)如图2中,作CK⊥BE′于K,求出CK,根据sin∠CBE′=$\frac{CK}{BC}$即可解决问题.
(3)根据图3、图4分别求出点P横坐标的最大值以及最小值即可解决问题.
解答 解:(1)如图1中,
∵AD′∥CE′,
∴∠AD′C=∠E′CD′=90°,
∵AC=2CD′,
∴∠CAD′=30°,
∴∠ACD′=90°-∠CAD′=60°,
∴α=60°.
(2)如图2中,作CK⊥BE′于K.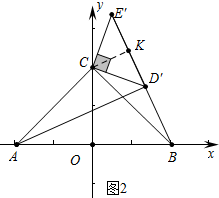
∵AC=BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴CD′=CE′=$\sqrt{2}$,
∵△CD′E′是等腰直角三角形,CD′=CE′=$\sqrt{2}$,
∴D′E′=2,
∵CK⊥D′E′,
∴KD′=E′K,
∴CK=$\frac{1}{2}$D′E′=1,
∴sin∠CBE′=$\frac{CK}{BC}$=$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$.
(3)如图3中,以C为圆心$\sqrt{2}$为半径作⊙C,当BE′与⊙C相切时AP最长,则四边形CD′PE′是正方形,作PH⊥AB于H.
∵AP=AD′+PD′=$\sqrt{6}$+$\sqrt{2}$,
∵cos∠PAB=$\frac{AP}{AB}$=$\frac{AH}{AP}$,
∴AH=2+$\sqrt{3}$,
∴点P横坐标的最大值为$\sqrt{3}$.
如图4中,当BE′与⊙C相切时AP最短,则四边形CD′PE′是正方形,作PH⊥AB于H.
根据对称性可知OH=$\sqrt{3}$,
∴点P横坐标的最小值为-$\sqrt{3}$,
∴点P横坐标的取值范围为-$\sqrt{3}$≤m≤$\sqrt{3}$.
点评 本题考查几何变换、等腰直角三角形的性质、锐角三角函数、勾股定理等知识,解题的关键是学会正确画出图形,学会分类讨论,找到点P横坐标的最大值、最小值是解题的难点,属于中考压轴题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案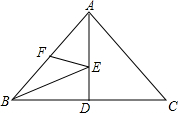 如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )
如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )| A. | 4 | B. | 4.8 | C. | 5 | D. | 5.4 |