题目内容
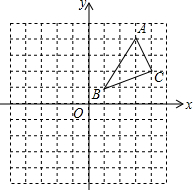如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（3，4）、B（1，1）、C（4，2）．（1）画出△ABC绕点B逆时针旋转90°后得到的△A1BC1，其中A、C分别和A1、C1对应．
（2）平移△ABC，使得A点落在x轴上，B点落在y轴上，画出平移后的△A2B2C2，其中A、B、C分别和A2B2C2对应．
（3）填空：在（2）的条件下，设△ABC，△A2B2C2的外接圆的圆心分别为M、M2，则MM2=
考点：作图-旋转变换,勾股定理,作图-平移变换
专题：作图题
分析：（1）根据网格结构找出点A、C绕点B逆时针旋转90°的对应点A1、C1的位置，再与点A顺次连接即可；
（2）根据网格结构找出点A、B、C平移后的对应点的位置，然后顺次连接即可；
（3）根据平移的性质，对应点的连续互相平行且相等可得MM2=AA2，再利用勾股定理列式计算即可得解．
（2）根据网格结构找出点A、B、C平移后的对应点的位置，然后顺次连接即可；
（3）根据平移的性质，对应点的连续互相平行且相等可得MM2=AA2，再利用勾股定理列式计算即可得解．
解答：
解：（1）△A1BC1如图所示；
（2）△A2B2C2如图所示；
（3）∵M、M2分别为△ABC，△A2B2C2的外接圆的圆心，
∴MM2=AA2，
由勾股定理得，AA2=
=
，
所以，MM2=
．
故答案为：
．
解：（1）△A1BC1如图所示；（2）△A2B2C2如图所示；
（3）∵M、M2分别为△ABC，△A2B2C2的外接圆的圆心，
∴MM2=AA2，
由勾股定理得，AA2=
| 12+42 |
| 17 |
所以，MM2=
| 17 |
故答案为：
| 17 |
点评：本题考查了利用旋转变换作图，利用平移变换作图，勾股定理，熟练掌握网格结构准确找出对应点的位置是解题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
如图，在△ABC，高线BE、AD相交于点O，∠BAE=45°．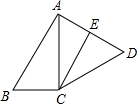
如图，四边形ABCD中，AC=CD，AB=2BC，∠BAC与∠B互余，CE∥BA，CE交AD于E，且CD2=CE2+DE2，求证：AD=
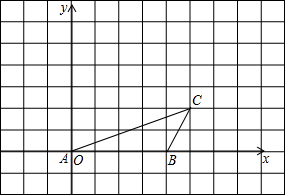如图，已知点A、B、C的坐标分别为（0，0）、（4，0）、（5，2），将△ABC绕点A按逆时针方向旋转90°得到△AB′C′．