题目内容
5.已知关于x的一元二次方程mx2-(m-1)x-1=0.(1)求证:这个一元二次方程总有两个实数根;
(2)若二次函数y=mx2-(m-1)x-1有最大值0,则m的值为-1;
(3)若x1、x2是原方程的两根,且$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=2x1x2+1,求m的值.
分析 (1)先计算判别式得到△=(m+1)2,根据非负数的性质即可得到△≥0,于是利用判别式的意义即可得到结论;
(2)根据二次函数的性质得m<0且$\frac{4m×(-1)-(m-1)^{2}}{4m}$=0,然后解方程即可;
(3)先根据根与系数的关系得到x1+x2=$\frac{m-1}{m}$,x1x2=-$\frac{1}{m}$,再把$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=2x1x2+1变形得到$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=2x1x2+1,则$\frac{(\frac{m-1}{m})^{2}-2•(-\frac{1}{m})}{-\frac{1}{m}}$=2•(-$\frac{1}{m}$)+1,然后解关于m的方程即可.
解答 (1)证明:m≠0,
△=(m-1)2-4m×(-1)
=(m+1)2,
∵(m+1)2≥0,即△≥0,
∴这个一元二次方程总有两个实数根;
(2)解:∵二次函数y=mx2-(m-1)x-1有最大值0,
∴m<0且$\frac{4m×(-1)-(m-1)^{2}}{4m}$=0,
∴m=-1;
故答案为-1.
(3)解:x1+x2=$\frac{m-1}{m}$,x1x2=-$\frac{1}{m}$,
∵$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=2x1x2+1,
∴$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=2x1x2+1,
∴$\frac{(\frac{m-1}{m})^{2}-2•(-\frac{1}{m})}{-\frac{1}{m}}$=2•(-$\frac{1}{m}$)+1,
整理得m2+m-1=0,
∴m=$\frac{-1+\sqrt{5}}{2}$或m=$\frac{-1-\sqrt{5}}{2}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式和二次函数的性质.

| A. | y随x的增大而减小 | B. | 图象位于一、三象限 | ||
| C. | 图象关于直线y=x对称 | D. | 点(-1,-2)在这个函数的图象上 |
| A. | c<b<a | B. | a<c<b | C. | b<c<a | D. | c<a<b |
| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | x≥-2 | B. | x≥-2且x≠-1 | C. | x≤-2且x≠-1 | D. | x≤-2 |
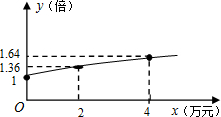 某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25%,设每双鞋的成本价为a元.
某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25%,设每双鞋的成本价为a元.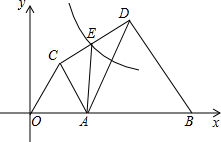 如图,B点的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边△OAC和等边△ABD,连接CD,E为CD的中点,双曲线y=$\frac{k}{x}$(x>0)经过点E,若AE=$\frac{\sqrt{79}}{2}$时,则k=10$\sqrt{3}$或15$\sqrt{3}$.
如图,B点的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边△OAC和等边△ABD,连接CD,E为CD的中点,双曲线y=$\frac{k}{x}$(x>0)经过点E,若AE=$\frac{\sqrt{79}}{2}$时,则k=10$\sqrt{3}$或15$\sqrt{3}$.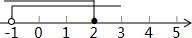 .
.