题目内容
19.已知点A(x1,y1),B(x2,y2)均在抛物线y=ax2+2ax-4(0<a<3)上,若x1>x2,x1+x2=1-a,则下列结论中正确的是( )| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小不确定 |
分析 可以运用“作差法”比较y1与y2的大小,y1与y2是自变量取x1、x2时,对应的函数值,代值后对式子因式分解,判断结论的符号即可.
解答 解:将x1代入抛物线,得y1=ax12+2ax1+4,将x2代入抛物线,得y2=ax22+2ax2-4,
y1-y2=a(x12-x22)+2a(x1-x2)
=a(x1-x2)(x1+x2)+2a(x1-x2)
=a(x1-x2)(x1+x2+2)
∵x1+x2=1-a,
∴y1-y2=a(x1-x2)(3-a),
∵0<a<3,x1>x2,
∴y1-y2>0,即y1>y2.
故选:A.
点评 本题考查了函数图象上的点的坐标与函数解析式的关系,在比较大小时用作差法是常用的比较方法.

练习册系列答案
相关题目
9.某市七天的空气质量指数分别是:28,45,28,45,28,30,53,这组数据的众数和中位数分别是( )
| A. | 28和45 | B. | 30和28 | C. | 45和28 | D. | 28和30 |
10.△ABC中,∠A=50°,∠B=70°,则∠C的度数是( )
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
14.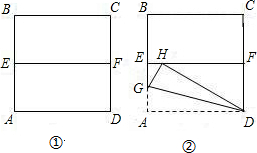 将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )
将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )
 将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )
将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )| A. | 8-4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 2$\sqrt{3}$-3 | D. | 4-2$\sqrt{3}$ |
4.下列运算中正确的是( )
| A. | a3+a3=a6 | B. | a2•a3=a5 | C. | (ab2)3=a3b3 | D. | a10÷a2=a5 |
8. 如图所示,正比例函数y1=k1x(k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象相交于A、B两点,其中A的横坐标为2,当y1>y2时,x的取值范围是( )
如图所示,正比例函数y1=k1x(k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象相交于A、B两点,其中A的横坐标为2,当y1>y2时,x的取值范围是( )
 如图所示,正比例函数y1=k1x(k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象相交于A、B两点,其中A的横坐标为2,当y1>y2时,x的取值范围是( )
如图所示,正比例函数y1=k1x(k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象相交于A、B两点,其中A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
9.-$\frac{1}{6}$的相反数是( )
| A. | -6 | B. | 6 | C. | -|-$\frac{1}{6}$| | D. | $\frac{1}{6}$ |
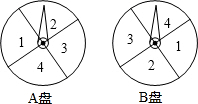 小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).
小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).