题目内容
11．把一副普通匹克牌中的13张黑桃牌洗匀后从中随机抽取一张，抽出的牌带有人像的概率是$\frac{3}{13}$．分析 由把一副普通匹克牌中的13张黑桃牌洗匀后从中随机抽取一张，其中带有人像的有3张，直接利用概率公式求解即可求得答案．
解答 解：∵把一副普通匹克牌中的13张黑桃牌洗匀后从中随机抽取一张，其中带有人像的有3张，
∴抽出的牌带有人像的概率是：$\frac{3}{13}$．
故答案为：$\frac{3}{13}$．
点评 此题考查了概率公式的应用．注意带有人像的牌有3张．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
1．
如图，AB∥CD，AF⊥AB，∠C=120°，则∠EAF的度数为（ ）
如图，AB∥CD，AF⊥AB，∠C=120°，则∠EAF的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
19．已知点A（x1，y1），B（x2，y2）均在抛物线y=ax2+2ax-4（0＜a＜3）上，若x1＞x2，x1+x2=1-a，则下列结论中正确的是（ ）
| A． | y1＞y2 | B． | y1=y2 | ||
| C． | y1＜y2 | D． | y1与y2的大小不确定 |
6．
如图，将正方体的平面展开图重新折成正方体后，“数”字对面的字是（ ）
如图，将正方体的平面展开图重新折成正方体后，“数”字对面的字是（ ）| A． | 喜 | B． | 欢 | C． | 我 | D． | 学 |
16．下列运算正确的是（ ）
| A． | 3x+2x=5x2 | B． | （a+2b）（a-2b）=a2-2b2 | C． | $\sqrt{8}$$-\sqrt{2}$=$\sqrt{6}$ | D． | $\sqrt{（-3）^{2}}$=3 |
3．
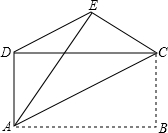如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则$\frac{AD}{AB}$的值为（ ）
如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则$\frac{AD}{AB}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |
20．
如图，O为原点，数轴上A，B，O，C四点，表示的数与点A所表示的数是互为相反数的点是（ ）
如图，O为原点，数轴上A，B，O，C四点，表示的数与点A所表示的数是互为相反数的点是（ ）| A． | 点B | B． | 点O | C． | 点A | D． | 点C |
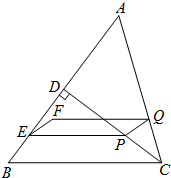如图，在△ABC中，AC=BC=5cm，AB=6cm，CD⊥AB于点D．动点P，Q同时从点C出发，点P沿线CD做依次匀速往返运动，回到点C停止；点Q沿折线CA-AD向终点D做匀速运动；点P，Q运动的速度都是5cm/s．过点P作PE∥BC，交AB于点E，连接PQ．当点P，E不重合且点P，Q不重合时，以线段PE，PQ为一组邻边作□PEFQ．设点P运动的时间为t（s），?PEFQ与△ABC重叠部分的面积为S（cm2）．