题目内容
16.概念:如果一个n×n矩阵(教材中表现为方格图)的每行,每列及两条对角线的元素之和都相等,且这些元素都是从1到n的自然数,这样的矩阵就称为n阶幻方.有关幻方问题的研究在我国已流传了两千多年,这是一类形式独特的填数字问题.下面介绍一种构造三阶幻方方法---杨辉法:(如图(1))口诀:“九子斜排,上下对易,左右相更,四维挺出”
学以致用:
(1)请你将下列九个数:-18、-16、-14、-12、-10、-8、-6、-4、-2,分别填入方格1中,使得每行、每列、每条对角线上的三个数之和都相等;
(2)将方格2中左边方格中的9个数填入右边方格中,使每一行、每一列、每条对角线中的三个数相加的和相等;
(3)将9个连续自然数填入方格3的方格内,使每一横行、每一竖行及两条对角线的3个数之和都等于60;
(4)用-3~5这九个数补全方格4中的幻方.
方格1
| 6 | 6 | 6 |
| 8 | 8 | 8 |
| 10 | 10 | 10 |
分析 (1)读题意,按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(2)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(3)根据已知,算出该9个连续自然数,按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论;
(4)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”,即可得出结论.
解答 解:(1)按照口诀:“九子斜排,上下对易,左右相更,四维挺出”
得出方格1:
| -8 | -18 | -4 |
| -6 | -10 | -14 |
| -16 | -2 | -12 |
得出结论:
| 8 | 10 | 6 |
| 6 | 8 | 10 |
| 10 | 6 | 8 |
9x=60×3,解得:x=20.
故这连续的九个数为:16,17,18,19,20,21,22,23,24.
按照口诀:“九子斜排,上下对易,左右相更,四维挺出”
得出方格3:
| 19 | 24 | 17 |
| 18 | 20 | 22 |
| 23 | 16 | 21 |
得出方格4:
| 0 | 5 | -2 |
| -1 | 1 | 3 |
| 4 | -3 | 2 |
点评 本题考查了一元一次方程的应用以及构造三阶幻方方法---杨辉法的应用,解题的关键是读懂题意,按照口诀一步步的变换.本题属于中档题型,有点难度,解题过程中有巧妙的办法,即利用给定的例题,再找出所以填写的9个数的中位数,看二者相差多少,再去给定的四维挺出表格中做相应的变动即可.

练习册系列答案
相关题目
6. 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠BAC=50°,则∠AEC的度数为( )| A. | 65° | B. | 75° | C. | 50° | D. | 55° |
4.两圆的半径分别为R和r,圆心距d=3,且R、r是方程x2-7x+10=0的两个根,则这两个圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |
 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.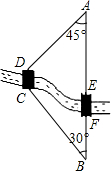 如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行. 如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.
如图,直线AE与CD相交于点B,∠DBE=50°,BF⊥AE,求∠CBF和∠DBF的度数.