题目内容
11.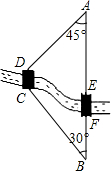 如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.(1)求桥DC与直线AB的距离;
(2)现在从A地到达B地可比原来少走多少路程?
(以上两问中的结果均精确到0.1km,参考数据:$\sqrt{2}$≈1.14,$\sqrt{3}$≈1.73)
分析 (1)要求桥DC与直线AB的距离,只要作CH⊥AB于点H,求出CH的长度即可,由BC和∠B可以求得CH的长,本题得以解决;
(2)要求现在从A地到达B地可比原来少走多少路程,只要求出AD与BC的和比AB-EF的长度多多少即可,由于DC=EF,有题意可以求得各段线段的长度,从而可以解答本题.
解答 解:(1)作CH⊥AB于点H,如下图所示,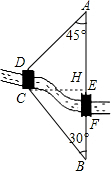
∵BC=12km,∠B=30°,
∴$CH=\frac{1}{2}BC=6$km,BH=$6\sqrt{3}$km,
即桥DC与直线AB的距离是6.0km;
(2)作DM⊥AB于点M,如下图所示,
∵桥DC和AB平行,CH=6km,
∴DM=CH=6km,
∵∠DMA=90°,∠B=45°,MH=EF=DC,
∴AD=$\frac{DM}{sin45°}=\frac{6}{\frac{\sqrt{2}}{2}}=6\sqrt{2}$km,AM=DM=6km,
∴现在从A地到达B地可比原来少走的路程是:(AD+DC+BC)-(AM+MH+BH)=AD+DC+BC-AM-MH-BH=AD+BC-AM-BH=$6\sqrt{2}+12-6-6\sqrt{3}$=6$+6\sqrt{2}-6\sqrt{3}$≈4.1km,
即现在从A地到达B地可比原来少走的路程是4.1km.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,作出合适的图形,利用数形结合的思想解答问题,注意ME=DC=EF.

练习册系列答案
相关题目
1.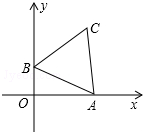 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
 如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )
如图,边长为2的等边△ABC的顶点A,B分别在x轴正半轴和y轴正半轴上运动,则动点C到原点O的距离的最大值是( )| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{6}-1$ | D. | $\sqrt{6}+1$ |
19.下列各组式子中,同类项是( )
| A. | 2a2b与3ab2 | B. | -x2y与4yx2 | C. | ax2与bx2 | D. | 3a2与4a3 |
6.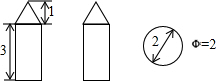 如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
 如图是某几何体的三视图及相关数据,则该几何体的表面积是( )
如图是某几何体的三视图及相关数据,则该几何体的表面积是( )| A. | 8π+$\sqrt{2}$π | B. | 7π+$\sqrt{2}$π | C. | 6π+$\sqrt{2}$π | D. | 7π2 |

 如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.