题目内容
1.先化简,再求值:$(\frac{6x}{3-x}-x+3)÷\frac{{{x^2}+9}}{x}÷\frac{3x}{{{x^2}-9}}$,其中x是方程x2+2x-3=0的解.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=[$\frac{6x}{3-x}$-$\frac{{(x-3)}^{2}}{3-x}$]•$\frac{x}{{x}^{2}+9}$•$\frac{(x+3)(x-3)}{3x}$
=$\frac{-6x-{x}^{2}-9+6x}{x-3}$•$\frac{x}{{x}^{2}+9}$•$\frac{(x+3)(x-3)}{3x}$
=$\frac{-({x}^{2}+9)}{x-3}$•$\frac{x}{{x}^{2}+9}$•$\frac{(x+3)(x-3)}{3x}$
=$\frac{-x-3}{3}$,
方程x2+2x-3=0可化为(x-1)(x+3)=0,解得x1=1,x2=-3,
∵当x=-3时原式无意义,
∴x=1,
∴原式=$\frac{-1-3}{3}$=-$\frac{4}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13. 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 两点之间直线最短 | D. | 垂线段最短 |
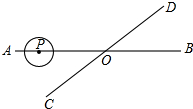 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.
如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的圆P的圆心在直线AB上,且与点O的距离为10cm,如果⊙P以2cm∕s的速度,沿由A向B的方向移动,那么4或6秒钟后⊙P与直线CD相切.